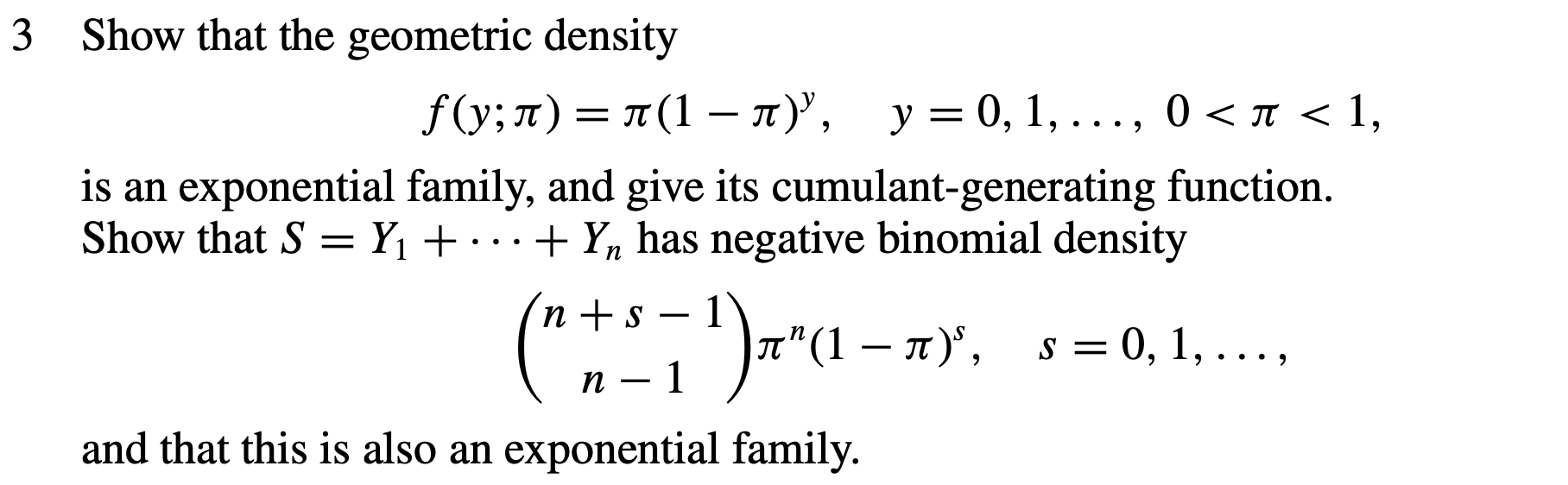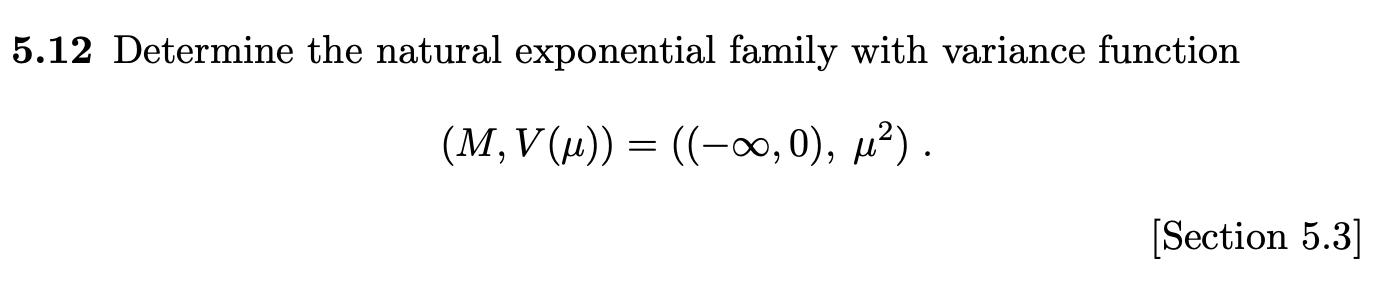Exercises B

Statistical Inference - Ph.D. in Economics, Statistics, and Data Science

Author

Affiliation

Tommaso Rigon

Università degli Studi di Milano-Bicocca

Homepage

Exercises

Davison (2003), Exercise 3, pag. 219

Pace and Salvan (1997), Problem 5.14

Davison (2003), Exercise 5, pag. 219

Davison (2003), Exercise 6, pag. 219

Pace and Salvan (1997), Problem 5.1

It is evident that the natural parameter space is non-empty, because 0 \in \tilde{\Theta}. Show that \tilde{\Theta} is a convex set, namely for all \theta_1, \theta_2 \in \tilde{\Theta} \subseteq{\mathbb{R}} \lambda \theta_1 + (1 - \lambda)\theta_2 \in \tilde{\Theta}, \qquad \text{for all }\quad 0 < \lambda < 1. Note that this implies \tilde{\Theta} must be an interval. Hint: recall that if \theta \in \tilde{\Theta} we have M_0(\theta) < \infty, thus combine the above equation with the inequality between the geometric and the arithmetic mean.

Pace and Salvan (1997), Problem 5.6 and 5.7

Pace and Salvan (1997), Problem 5.12

References

Davison, A. C. (2003), Statistical Models, Cambridge University Press.

Pace, L., and Salvan, A. (1997), Principles of statistical inference from a Neo-Fisherian perspective, Advanced series on statistical science and applied probability, World Scientific.