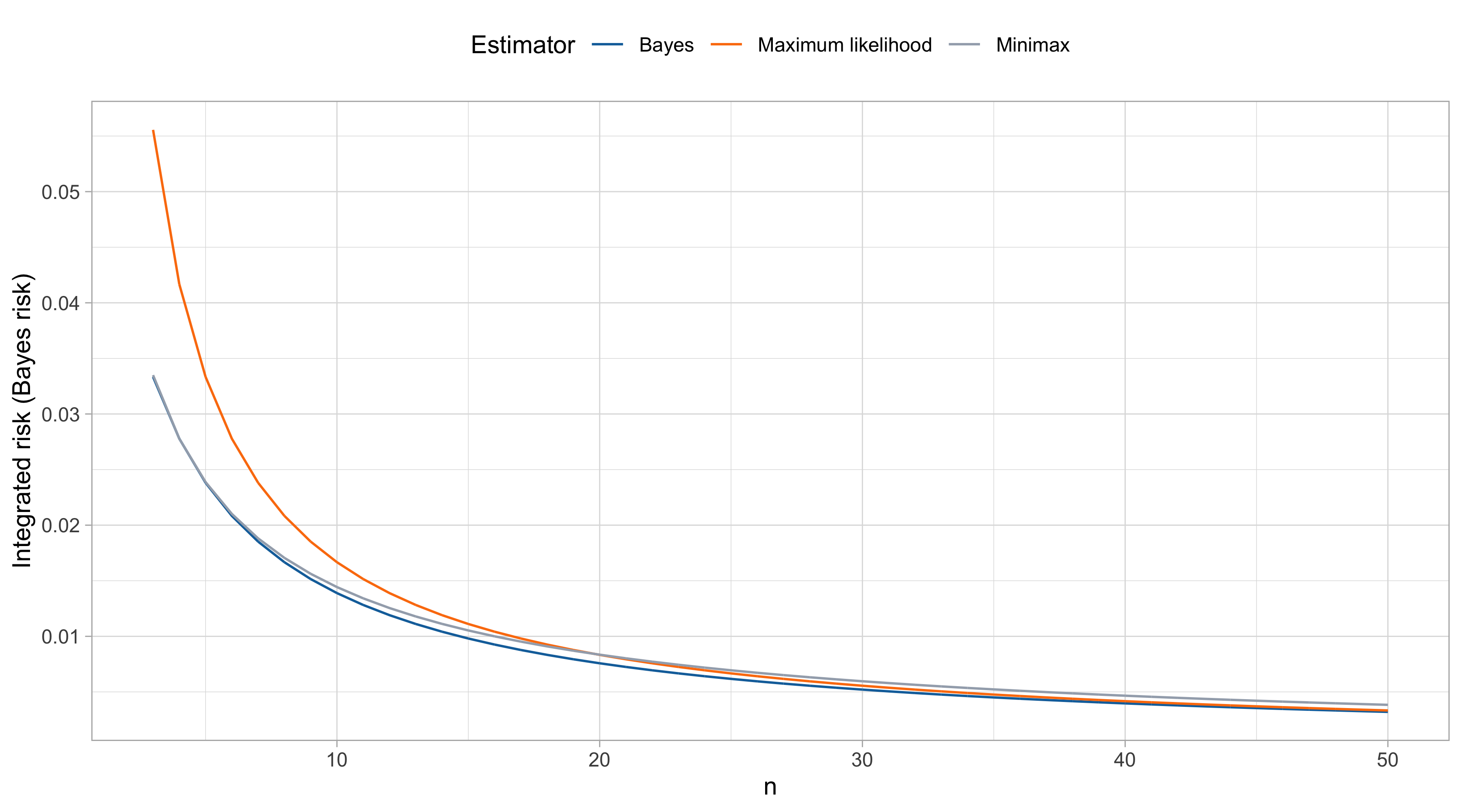
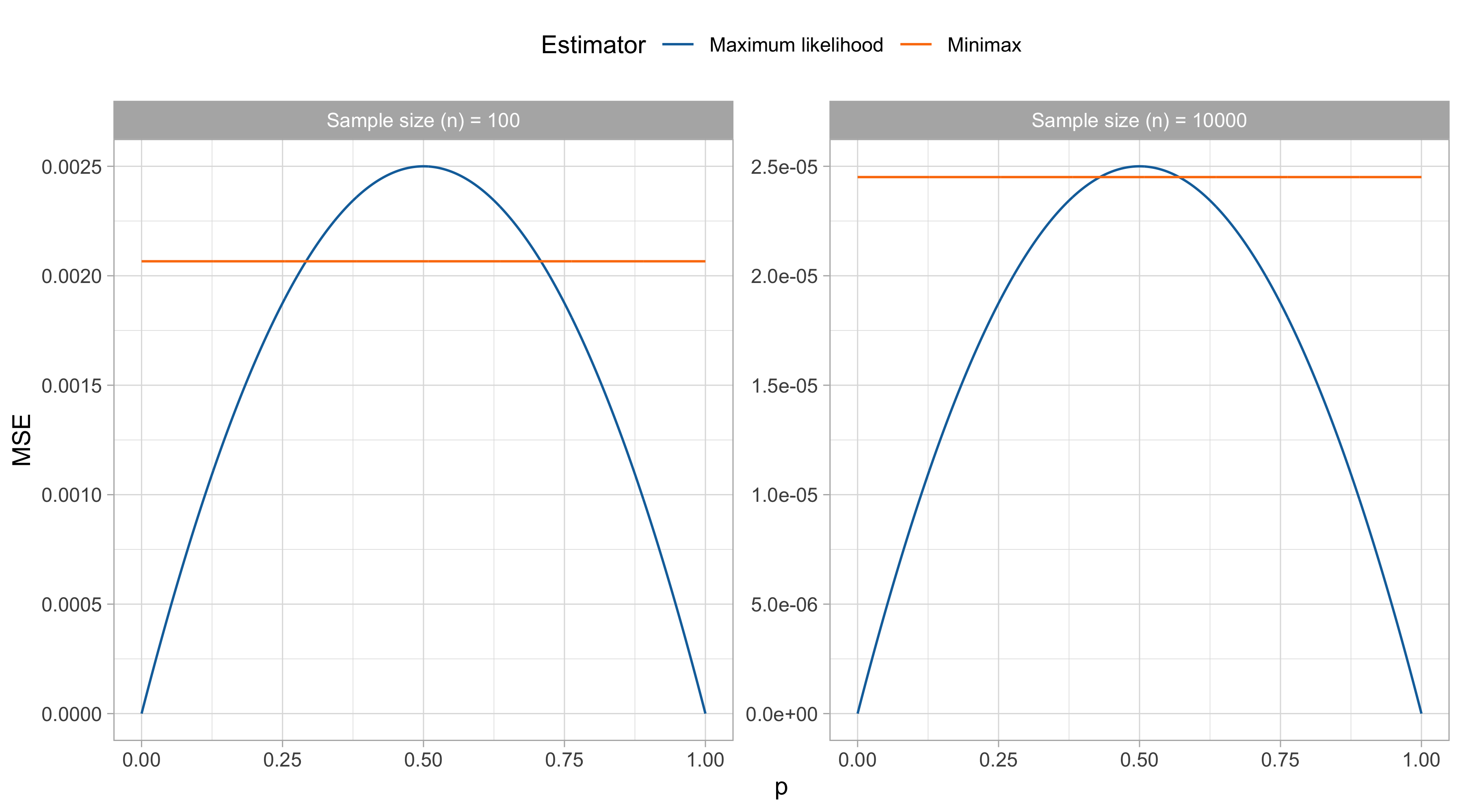
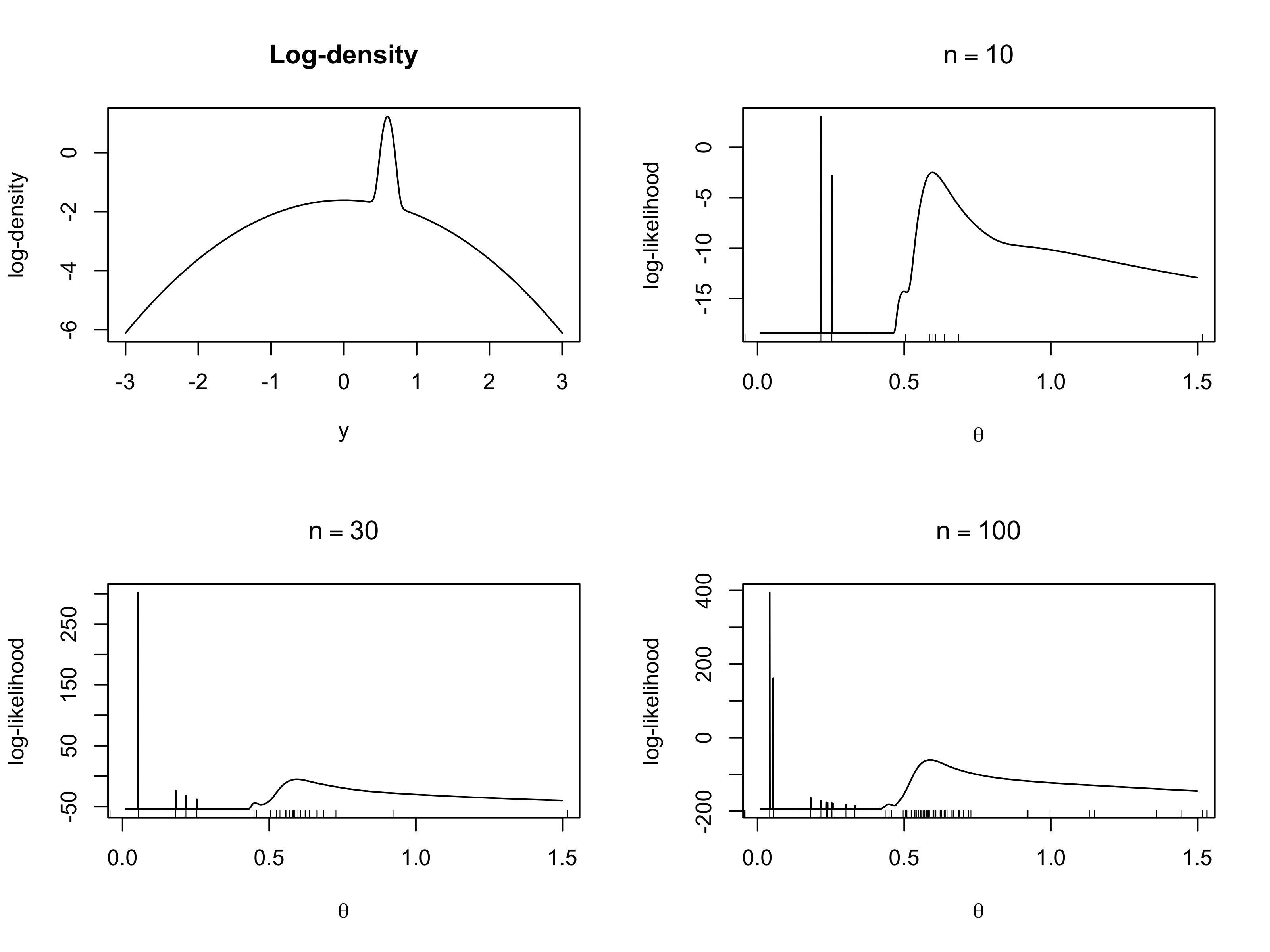
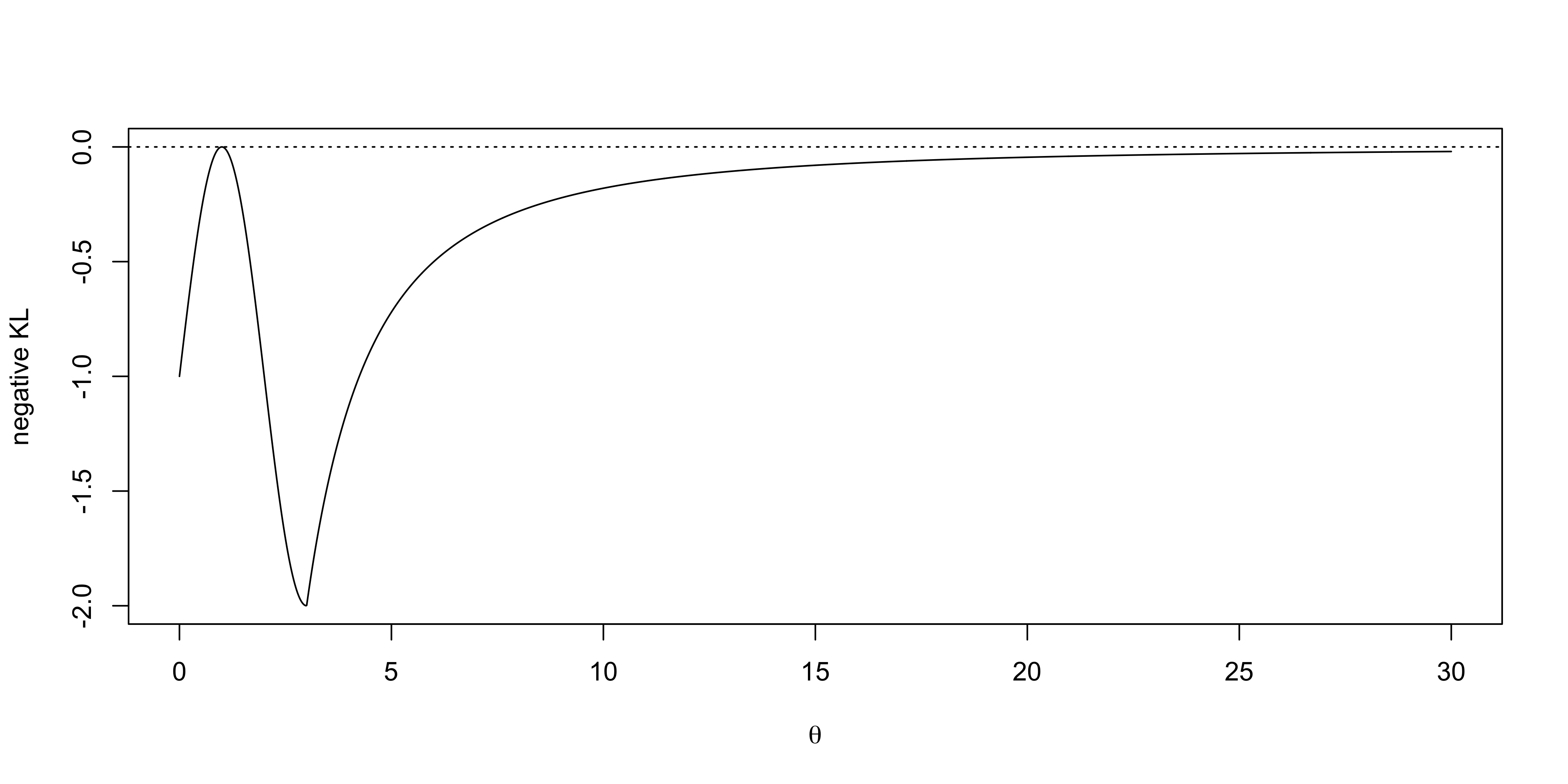
Agresti, A. (2015), Foundations of Linear and Generalized Linear Models, Wiley.
Casella, G., and Berger, R. L. (2002), Statistical Inference, Duxbury.
Davison, A. C. (2003), Statistical Models, Cambridge University Press.
Diaconis, P., and Ylvisaker, D. (1979), “Conjugate prior for exponential families,” The Annals of Statistics, 7, 269–292.
Efron, B. (1975), “Defining the curvature of a statistical problem (with applications to second order efficiency),” The Annals of Statistics, 3, 1189–1242.
Efron, B. (2010), Large Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction, Institute of mathematical statistics monographs, Leiden: Cambridge University Press.
Efron, B., and Hastie, T. (2016), Computer Age Statistical Inference, Cambridge University Press.
Efron, B., and Hinkley, D. V. (1978), “Assessing the accuracy of the maximum likelihood estimator: Observed vs fisher information,” Biometrika, 65, 457–482.
Efron, B., and Morris, C. (1975), “Data analysis using Stein’s estimator and its generalizations,” Journal of the American Statistical Association, 70, 311–319.
Firth, D. (1993), “Bias reduction of maximum likelihood estimates,” Biometrika, 80, 27–38.
Godambe, V. P. (1960), “An optimum property of regular maximum likelihood estimation,” Annals of Mathematical Statistics, 31, 1208–1211.
Huber, P. J. (1967), “The behavior of maximum likelihood estimates under nonstandard conditions,” in Proceedings of the fifth berkeley symposium on mathematical statistics and probability.
James, W., and Stein, C. (1961), “Estimation with quadratic loss,” in Proc. Fourth berkeley symposium, University of California Press, pp. 361–380.
Lehmann, E. L., and Casella, G. (1998), Theory of Point Estimation, Second Edition, Springer.
Pace, L., and Salvan, A. (1997), Principles of statistical inference from a Neo-Fisherian perspective, Advanced series on statistical science and applied probability, World Scientific.
Robert, C. P. (1994), The Bayesian Choice: from decision-theoretic foundations to computational implementation, Springer.
Stein, C. (1956), “Inadmissibility of the usual estimator of the mean of a multivariate normal distribution,” in Proc. Third Berkeley Symposium, University of California Press, pp. 197–206.
van der Vaart, A. W. (1998), Asymptotic Statistics, Cambridge University Press.
White, H. (1980), “A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity,” Econometrica, 4, 817–838.