Statistica I

Esame 17 Novembre 2023

Autore/Autrice
Affiliazione

Tommaso Rigon

DEMS

Problema 1

I dati provengono da uno studio condotto da Charles Darwin nel 1875 riguardante i metodi di impollinazione. Un insieme di n = 15 coppie di piantine della stessa età, la prima ottenuta tramite impollinazione incrociata (cross-fertilization) e l’altra tramite auto-impollinazione (self-fertilization), sono state coltivate in condizioni quasi identiche.

I dati corrispondono alle altezze finali (in pollici) di ciascuna coppia di piante (cross e self), dopo un determinato periodo di tempo. La variabile diff = cross - self è pari alla differenza delle prime due variabili.

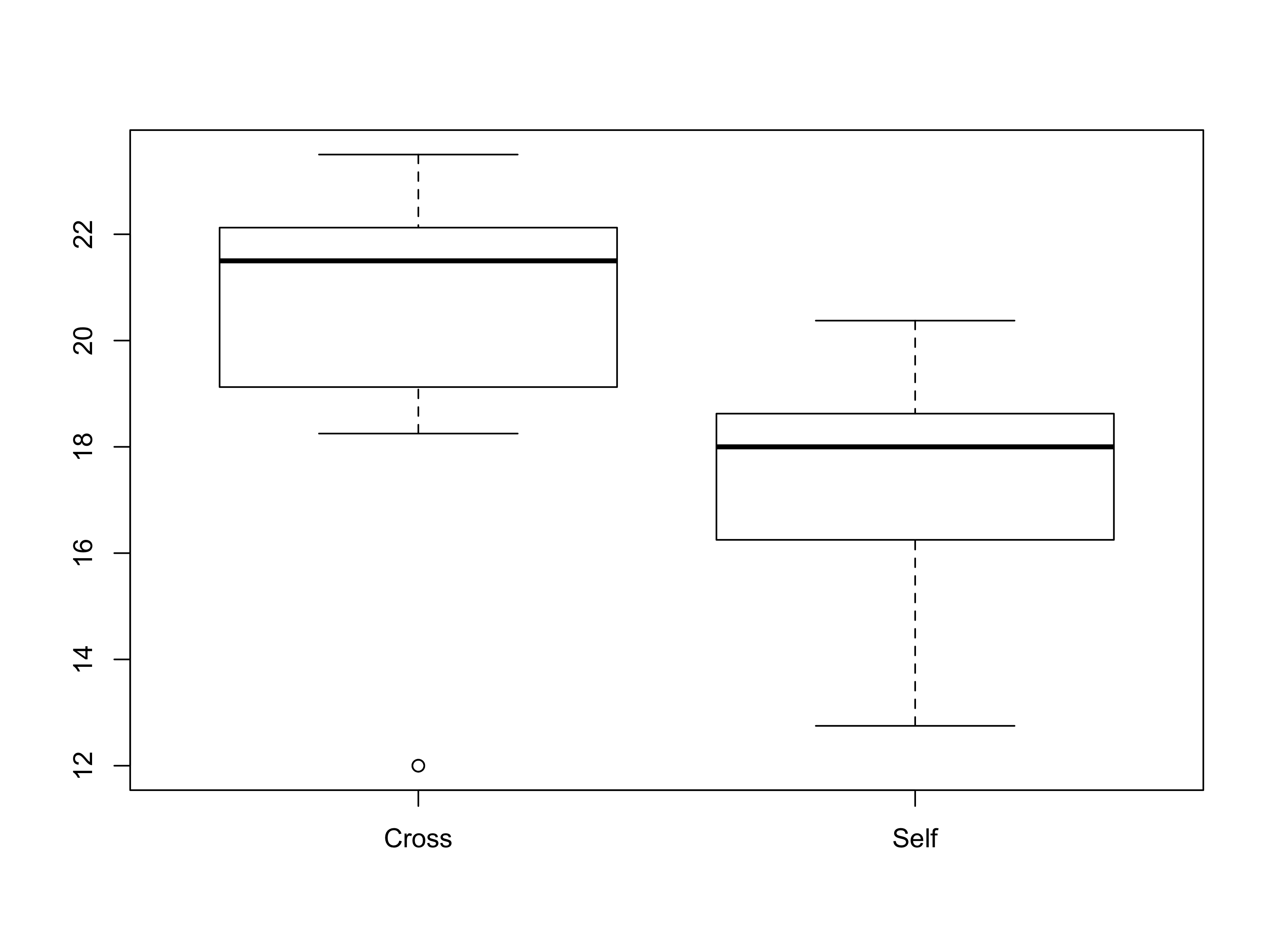
Coppia cross self diff
1 23.500 17.375 6.125
2 12.000 20.375 -8.375
3 21.000 20.000 1.000
4 22.000 20.000 2.000
5 19.125 18.375 0.750
6 21.500 18.625 2.875
7 22.125 18.625 3.500
8 20.375 15.250 5.125
9 18.250 16.500 1.750
10 21.625 18.000 3.625
11 23.250 16.250 7.000
12 21.000 18.000 3.000
13 22.125 12.750 9.375
14 23.000 15.500 7.500
15 12.000 18.000 -6.000

Si è interessati a verificare se l’impollinazione incrociata consente alle piante di avere maggior vigore, misurata in termini di altezza.

  1. Si calcolino medie e varianze delle variabili cross e self. Si calcoli quindi la media della variabile diff.

  2. Si confrontino tra loro le distribuzioni cross e self tramite due boxplot, evidenziando la presenza di eventuali valori anomali. Si riportino i valori di mediana e quartili delle due distribuzioni.

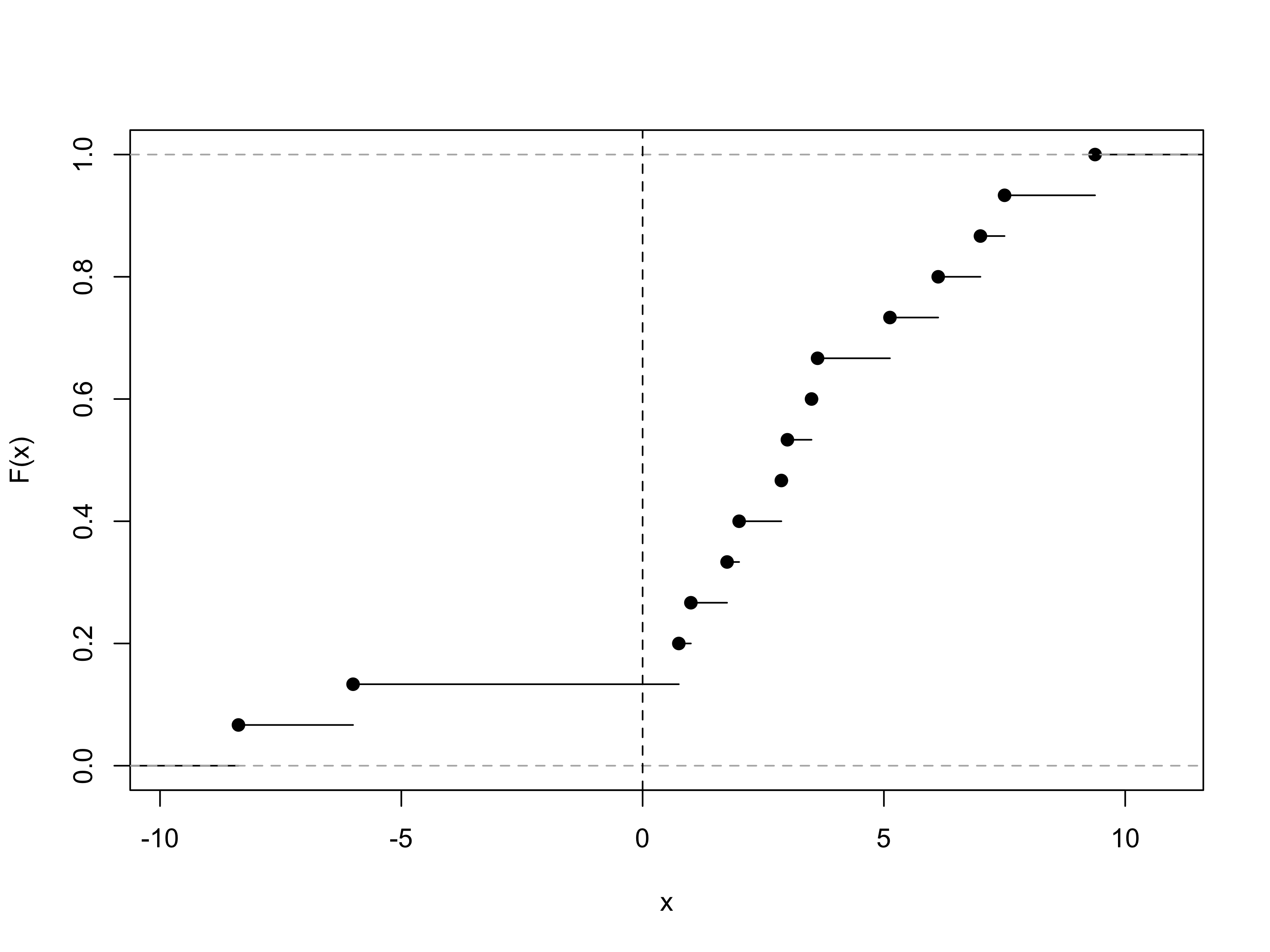
  3. Si stabilisca se le medie delle distribuzioni cross e self sono diverse tra loro, facendo uso di opportuni indici che tengano conto della variabilità dei dati. Si commentino i risultati nel contesto del problema.

  4. Si disegni la funzione di ripartizione F(\cdot) della variabile diff. Si calcoli il valore di F(0) e si commenti il risultato nel contesto del problema.

Statistiche descrittive delle variabili cross, self e diff.

##      Media cross  Media self Media diff Varianza cross Varianza self
## [1,]     20.19167     17.575   2.616667       12.21014       3.92875

Ulteriori statistiche descrittive per le variabili cross e self:

Primo quartile, mediana, terzo quartile della variabile cross

##    25%    50%    75% 
## 19.125 21.500 22.125

Primo quartile, mediana, terzo quartile della variabile self

##    25%    50%    75% 
## 16.250 18.000 18.625

Confronto tra i due boxplot, da cui è possibile notare la presenza di due outlier. Trattandosi di un confronto, i due boxplot andavano disegnati nello stesso grafico.

La dipendenza in media può essere misurata tramite l’indice \eta^2, il cui calcolo richiede alcuni passaggi intermedi. Era possibile far uso di appropriati indici alternativi non menzionati nel corso. Tuttavia, indici quali il coefficiente di variazione non misurano la dipendenza in media, bensì esclusivamente la variabilità dei dati.

Devianza entro i gruppi:

## [1] 242.0833

Devianza tra i gruppi:

## [1] 51.35208

Devianza totale:

## [1] 293.4354

Indice \eta^2 è quindi pari a:

## [1] 0.175003

Se ne deduce una lieve dipendenza in media, che a sua volta implica che il metodo di impollinazione incrociata consente alle piante di avere maggior vigore. Questo risultato sembra essere in parziale contraddizione con quanto mostrato dai boxplot, che evidenziano una dipendenza in distribuzione tra i due gruppi molto più marcata. È tuttavia possibile che \eta^2 sia relativamente basso a causa dei due outlier (entrambi pari a 12) presenti nella variabile cross.

Funzione di ripartizione empirica della variabile diff:

La linea verticale tratteggiata indica il valore della funzione di ripartizione valutata in 0, ovvero F(0):

## [1] 0.1333333

Di consequenza, la maggioranza delle piantine cross, ovvero circa l’87\%, assume valori maggiori di quelle self, dimostrando nuovamente una forte dipendenza. In altri termini, l’impollinazione incrociata sembra essere associata a piantine di maggior vigore.

Problema 2

Si vuole analizzare la potenzialità di un fertilizzante nel velocizzare la crescita degli alberi. Per n = 10 alberi si rileva la quantità di fertilizzante che è stata usata nel terreno su cui ciascun alberto è stato coltivato, espressa in mg per g, e la velocità di crescita dell’albero, in cm al mese. Le osservazioni sono riportate nella tabella seguente.

fertilizzante crescita
8.31 7.51
9.15 9.04
7.77 6.64
4.39 4.65
0.31 1.85
8.94 8.37
5.13 5.10
1.39 2.61
4.30 6.01
2.03 4.30

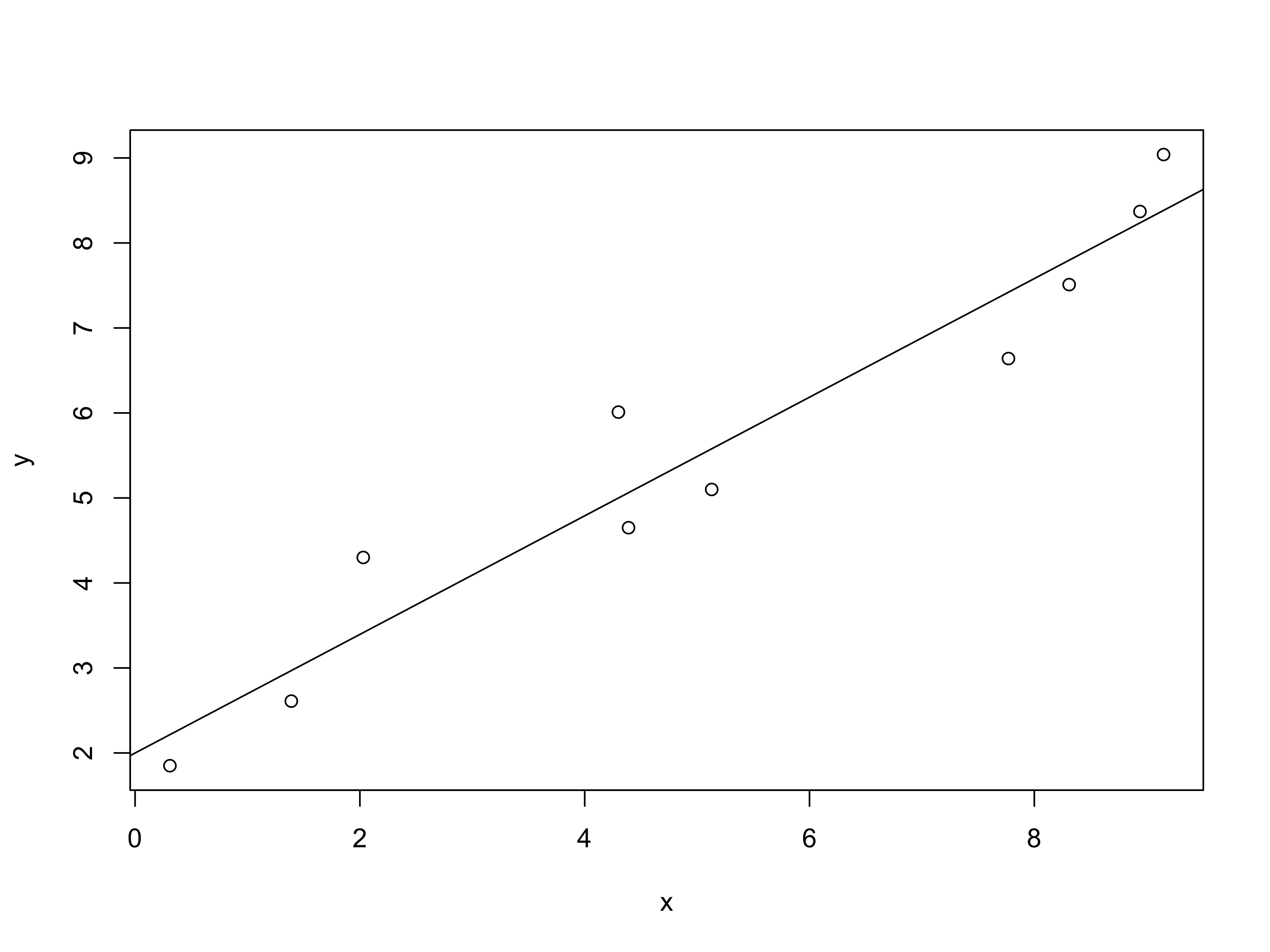
  1. Si rappresentino graficamente le variabili fertilizzante e crescita tramite un diagramma a dispersione.

  2. Si specifichi un modello di regressione per studiare la crescita media in funzione della quantità di fertilizzante. Si stimi tale modello.

  3. Si ottenga un indice di bontà d’adattamento per il modello stimato al punto precedente. Si ottenga inoltre la varianza residuale di tale modello.

  4. La crescita media aumenta con la quantità di fertilizzante? Si argomenti, basandosi sui risultati ottenuti ai punti precedenti.

  5. Si dica qual è la crescita media in assenza di fertilizzante. Inoltre, quanto fertilizzante è necessario affinchè la crescita media sia pari a 5cm al mese?

Grafico a dispersione (richiesto), con retta di regressione stimata (non richiesta)

Alcune utili statistiche descrittive preliminari:

##      Media fert. Media crescita Varianza fert. Varianza crescita Covarianza Correlazione
## [1,]       5.172          5.608       9.580736          5.024876   6.684884    0.9634557

Coefficienti del modello di regressione stimati (\hat{\alpha},\hat{\beta}):

## (Intercept)           x 
##   1.9992772   0.6977422

Indice R^2 e varianza residuale:

## [1] 0.9282469 0.3605502

La quantità fertilizzante sembra pertanto comportare un aumento della crescita. Ciò si deduce dal fatto che il coefficiente \hat{\beta} calcolato in precedenza è positivo, congiuntamente al fatto che il coefficiente di correlazione \rho è grande e positivo.

Si noti il valore di R^2, da solo, non consente di stabilire se esiste una relazione positiva o negativa tra le due variabili.

Previsione della crescita quando x = 0 coincide con \hat{\alpha}, ovvero:

## (Intercept) 
##    1.999277

Valore del fertilizzante tale per cui la crescita è pari a 5:

## (Intercept) 
##    4.300618

Problema 3

Si risponda a tutti i seguenti quesiti di carattere teorico.

  1. Dopo averne dato la definizione, si dimostri che la media geometrica \mathbb{G} di un insieme di dati x_1,\dots,x_n a valori strettamente positivi è minore o uguale della loro media aritmetica \bar{x}. Si menzionino esplicitamente i risultati teorici utilizzati nella dimostrazione.

  2. Si enunci e si dimostri il teorema di scomposizione della devianza.

  3. Nel contesto delle tabelle di contingenza, si dimostri che le seguenti formule del \chi^2 sono equivalenti:

\chi^2 = \sum_{i=1}^h\sum_{j=1}^k \frac{(n_{ij} - \hat{n}_{ij})^2}{\hat{n}_{ij}} = n\left[\sum_{i=1}^h\sum_{j=1}^k\left(\frac{f_{ij}^2}{f_{i+}f_{+j}}\right) - 1\right].

La soluzione di questi esercizi è presente nelle slides oppure è stata spiegata in classe.