Problema 1
Nell’A.A. 2024/25, durante il corso Statistica I, è stato condotto un esperimento. Agli studenti presenti è stato chiesto per due volte di indovinare il numero di biglie presenti in una bottiglia, la quale conteneva 282 biglie. Al primo tentativo (x) non è stata fornita alcuna informazione di supporto, mentre al secondo tentativo (y) sono state fornite delle informazioni aggiuntive, come la dimensione delle biglie e la capacità della bottiglia.
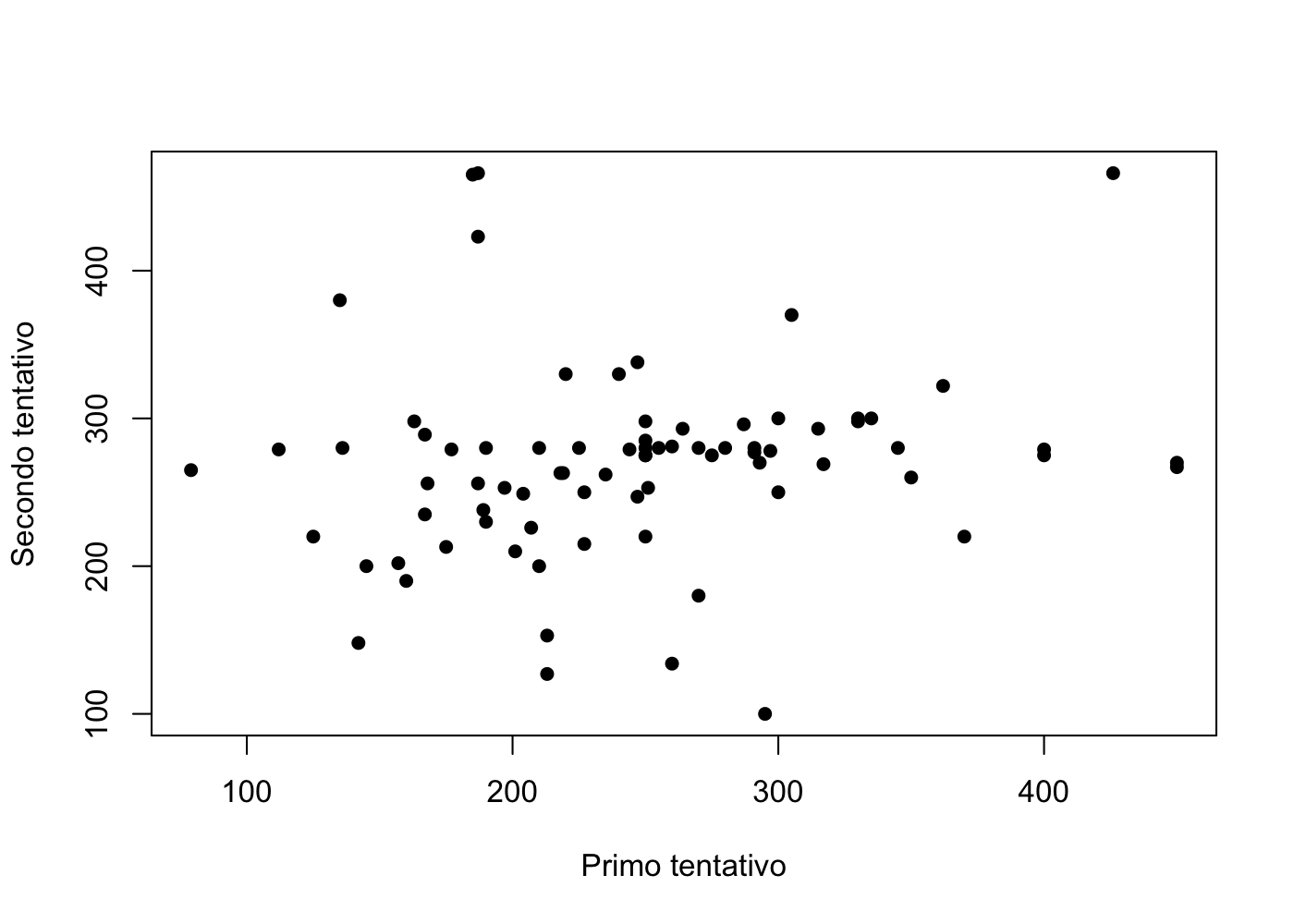
Dopo alcune analisi preliminari, sono state ritenute valide un totale di n = 79 risposte. Tali risposte sono state rappresentate nel seguente diagramma a dispersione.
Vengono inoltre riportate nel seguito alcune quantità di potenziale interesse:
\sum_{i=1}^{79} x_i = 19451, \quad \sum_{i=1}^{79} x_i^2 = 5255977, \quad \sum_{i=1}^{79} y_i = 21256, \quad \sum_{i=1}^{79} y_i^2 = 6054602,
\sum_{i=1}^{79} x_i y_i = 5293892, \quad \frac{1}{79}\sum_{i=1}^{79} y_i^3 = 23072804.33, \quad \frac{1}{79}\sum_{i=1}^{79} y_i^4 = 7360399442.
Si calcolino le varianze delle variabili primo tentativo e secondo tentativo e la loro correlazione.
Si consideri il seguente modello di regressione lineare:
y_i = \alpha + \beta x_i + \epsilon_i, \qquad i=1,\dots,79.
Si ottengano delle stime per \alpha e \beta nel modo che si ritiene più opportuno.
Si fornisca quindi un’interpretazione per i coefficienti stimati al punto precedente. In che modo gli studenti hanno cambiato la loro opinione, se lo hanno fatto?
Si calcoli la varianza residuale del modello stimato. Inoltre, sapendo che x_9 = 187 e y_9 = 466, a quanto ammonta il residuo corrispondente r_9?
Si ottenga l’indice di bontà di adattamento R^2 e lo si interpreti nel contesto del problema.
Si calcoli l’indice di curtosi di Pearson \kappa per la variabile secondo tentativo e se ne dia un’interpretazione. Suggerimento: si ricordi che (a - b)^4 = a^4 - 4a^3b + 6 a^2 b^2 - 4 a b^3 + b^4.
- Questo primo punto è stato svolto correttamente da quasi la totalità degli iscritti alla prova. Alcuni studenti non hanno però calcolato la correlazione. A partire dai valori riportati nel testo dell’esame, a meno di piccole discrepanze dovute all’approssimazione usata, si otteneva infatti che:
| Media x (primo tentativo) |
246.215190 |
| Media y (secondo tentativo) |
269.063291 |
| Varianza x (primo tentativo) |
5909.434706 |
| Varianza y (secondo tentativo) |
4245.477007 |
| Covarianza(x, y) |
763.821823 |
| Correlazione(x,y) |
0.152495 |
Era possibile stimare \alpha e \beta tramite minimi quadrati, usando le formule consuete, ottenendo:
\hat{\beta}= 0.129255, \quad \hat{\alpha} = 237.238837.
Anche questa domanda è stata svolta correttamente dalla larga maggioranza degli studenti. Vi sono stati alcuni (pochi) errori grossolani, come ad es. l’uso di formule sbagliate, errori di conto banali, etc.
L’interpretazione dei coefficienti stimati ha causato molte difficoltà. Nella maggior parte degli esami è stato osservato che al secondo tentativo le stime risultavano più accurate rispetto al primo, ovvero più vicine a 282, come emerge dalle medie. Inoltre, è stato talvolta notato che la varianza del secondo tentativo è inferiore a quella del primo. Sebbene queste affermazioni siano corrette, esse non rispondono alla domanda posta, che riguardava specificamente l’interpretazione dei coefficienti e del modello stimato. Ecco, ad esempio, quanto si poteva commentare:
- Anzitutto, si poteva notare che \hat{\alpha} rappresenta la stima, al secondo tentativo, di un ipotetico studente che al primo tentativo avesse dichiarato “0”. Sebbene si tratti di un caso poco realistico, \hat{\alpha} ha proprio questo significato. Inoltre, \hat{\beta} = 0.129 implica che, in media, al crescere del valore del primo tentativo, aumenta anche il valore stimato del secondo. Più precisamente, ogni biglia aggiuntiva nel primo tentativo corrisponde, in media, a un incremento di 0.129 biglie nel secondo tentativo.
- Ciò che in pochi hanno commentato è il fatto che \hat{\beta} < 1, analogamente a quanto avviene nei dati di Galton relativi alle altezze di padri e figli. Combinando questo aspetto con la stima di \hat{\alpha}, si deduce che coloro che avevano sottostimato il numero di biglie al primo tentativo (ad esempio, x_1 = 100) hanno in media aumentato la loro stima al secondo tentativo (\hat{y}_1 = 250.16). Viceversa, coloro che avevano sovrastimato il numero di biglie al primo tentativo (ad esempio, x_2 = 400) hanno in media diminuito la loro stima al secondo tentativo (\hat{y}_2 = 288.9407).
- Complessivamente, gli studenti hanno cambiato opinione. Si osservi che una perfetta coerenza con la propria opinione precedente si sarebbe ottenuta nel caso in cui \hat{\alpha} = 0, \hat{\beta} = 1 e, soprattutto, R^2 = 1, cioè con dati perfettamente allineati alla bisettrice. Tuttavia, si riscontra che R^2 \approx 0.02, oltre a valori differenti per \hat{\alpha} e \hat{\beta}. Pertanto, la tendenza media a correggere quanto fatto al primo tentativo (cioè quanto descritto al punto b.) spiega solo una piccola frazione della variabilità di y. Gli studenti hanno effettivamente cambiato opinione, ma lo hanno fatto senza considerare in modo significativo quanto stimato nel primo tentativo.
Usando le formule illustrate a lezione, la varianza residuale si calcola essere pari a \text{var}(r) = 4146.749496. Inoltre, si ottiene che il valore previsto è \hat{y}_9 = 261.409453 e pertanto il residuo corrispondente è r_9 = y_9 - \hat{y}_9 = 204.590547.
Si ottiene che l’indice di bontà d’adattamento è pari a R^2 = \rho^2 = 0.023255. Come detto in precedenza, questo significa la tendenza media a correggere quanto fatto al primo tentativo spiega solo una piccola frazione della variabilità di y. Gli studenti hanno effettivamente cambiato opinione, ma lo hanno fatto senza considerare in modo significativo quanto stimato nel primo tentativo.
Questo esercizio coinvolgeva numeri molto grandi e, di conseguenza, moltissimi hanno commesso errori di calcolo. L’indice di curtosi di Pearson si otteneva a partire dai dati a disposizione attraverso la seguente scomposizione:
\kappa_y = \frac{1}{\sigma_y^4}\frac{1}{n}\sum_{i=1}^n(y_i - \bar{y})^4 = \frac{1}{\sigma_y^4}\left[\frac{1}{n}\sum_{i=1}^ny_i^4 - 4 \bar{y}\frac{1}{n} \sum_{i=1}^ny_i^3 + 6 \bar{y}^2\frac{1}{n}\sum_{i=1}^ny_i^2 - 4 \bar{y}^3 \frac{1}{n} \sum_{i=1}^n y_i + \bar{y}^4\right].
Da questa scrittura, facendo attenzione a non dimenticare alcun termine, si otteneva che \kappa_y = 5.29635, che implica un eccesso di curtosi (code pesanti) essendo che \kappa_y > 3.
Problema 2
Durante l’A.A. 2024/25 agli studenti del corso di Statistica I è stato chiesto di identificare la tipologia di 5 diversi indici. I risultati di questo esperimento didattico sono riportati nella tabella seguente, che mostra le frequenze congiunte delle variabili domanda e risposta (variabile binaria: 0 risposta errata, 1 risposta corretta). La numerosità campionaria n = 310 rappresenta il numero complessivo di risposte fornite.
| a. (indice pari a 0) |
48 |
12 |
| b. (varianza) |
21 |
42 |
| c. (differenza semplice media) |
43 |
17 |
| d. (media geometrica) |
16 |
45 |
| e. (scarto interquartile) |
61 |
5 |
Si ottengano le frequenze relative della variabile risposta condizionatamente a ciascun valore della variabile domanda.
Si stabilisca quale tra le distribuzioni della variabile risposta, condizionatamente a ciascun valore della variabile domanda, risulta maggiormente eterogenea.
(Teoria) Sia y una variabile binaria, ovvero i cui valori y_1,\dots,y_n sono pari 0 oppure a 1. Il valore 0 ha frequenze relativa pari f_0 mentre il valore 1 ha frequenze relativa f_1. Si mostri che in tal caso l’indice di eterogeneità Gini è pari a 2 volte la varianza, ovvero:
G = 2\: \text{var}(y).
Si stabilisca, tramite opportuni indici, se la variabile risposta è dipendente in distribuzione dalla variabile domanda. Si fornisca un’interpretazione di questi risultati.
Si stabilisca, tramite opportuni indici, se la variabile risposta è dipendente in media dalla variabile domanda. Si fornisca un’interpretazione di questi risultati.
- Questa prima domanda ha, con mia sorpresa, causato qualche difficoltà. Erano richieste le frequenze relative condizionate, le quali sono pari a
| a |
0.800 |
0.200 |
| b |
0.333 |
0.667 |
| c |
0.717 |
0.283 |
| d |
0.262 |
0.738 |
| e |
0.924 |
0.076 |
Si noti che ciascuna riga somma ad 1, pertanto questa tabella colleziona in forma compatta 5 distribuzioni di frequenza.
- Una variabile qualitativa è tanto più eterogenea quanto più le sue frequenze relative risultano simili tra loro. Era richiesto identificare la più eterogenea tra le 5 distribuzioni calcolate al punto 1. Come hanno fatto molti, si potevano calcolare gli indici di eterogeneità di Gini (o di Shannon) per ciascuna variabile, ottenendo:
| a |
0.800 |
0.200 |
0.320 |
| b |
0.333 |
0.667 |
0.444 |
| c |
0.717 |
0.283 |
0.406 |
| d |
0.262 |
0.738 |
0.387 |
| e |
0.924 |
0.076 |
0.140 |
Da ciò si evince che la risposta b era la più eterogenea, avendo il valore di Gini maggiore. In questo caso molto semplice, è stata accettata come corretta anche la risposta di chi si è limitato a confrontare le frequenze relative, notando che la distanza tra 0.333 e 0.667 era la più piccola. Tuttavia, non è stata considerata corretta la risposta di chi ha scritto semplicemente “b” senza fornire alcuna giustificazione.
Questa domanda era leggermente più complessa delle altre e serviva per accedere alle valutazioni più alte. Come mostrato anche durante le esercitazioni, la varianza di una variabile binaria è data da:
\text{var}(y) = f_1(1 - f_1) = f_0(1 - f_0),
ricordando che f_1 = 1 - f_0. Di conseguenza:
2\text{var}(x) = f_1(1 - f_1) + f_0(1 - f_0) = f_0(1 - f_0) + f_1(1 - f_1) = \sum_{j=0}^1 f_j(1 - f_j) = G.
Questa era una semplice dimostrazione. Sono state accettate anche dimostrazioni alternative, ovviamente purché corrette.
Questa era una domanda “standard”, affrontata varie volte a lezione. Per verificare l’indipendenza in distribuzione, era possibile utilizzare l’indice di connessione \chi^2. A tal fine, si potevano anzitutto calcolare le frequenze attese, che sono date da:
| a |
36.581 |
23.419 |
| b |
38.410 |
24.590 |
| c |
36.581 |
23.419 |
| d |
37.190 |
23.810 |
| e |
40.239 |
25.761 |
Dalla tabella, si concludeva, dopo qualche calcolo, che \chi^2 = 90.612537 e inoltre che \chi^2_\text{norm} = 0.292299. Di conseguenza, si osserva una discreta dipendenza in distribuzione. Questo implica semplicemente che la frazione di risposte corrette dipende dalla domanda, suggerendo che probabilmente le domande presentavano livelli di difficoltà diversi tra loro.
- Questa domanda è stata molto problematica ma era in effetti leggermente più complessa dal punto di vista concettuale. Alcuni studenti hanno calcolato le medie delle frequenze assolute, che ovviamente non ha alcun senso. Veniva richiesto di valure la dipendenza in media della variabile
risposta in funzione della variabile domanda. Si noti che la variabile risposta è numerica e assume i valori 0 ed 1. Di conseguenza, le frequenze relative condizionate della risposta corretta corrispondono alle medie del gruppo, mentre le varianze condizionate sono pari alla metà dei coefficienti di Gini precedentemente calcolati. In primo luogo, andava pertanto ottenuta la seguente tabella:
| a |
0.200 |
0.320 |
0.160 |
60 |
9.600 |
| b |
0.667 |
0.444 |
0.222 |
63 |
14.000 |
| c |
0.283 |
0.406 |
0.203 |
60 |
12.183 |
| d |
0.738 |
0.387 |
0.193 |
61 |
11.803 |
| e |
0.076 |
0.140 |
0.070 |
66 |
4.621 |
Si noti inoltre che \bar{x} = 0.390323. A partire da questa tabella, si otteneva che: \mathscr{D}^2_\text{tr} = \sum_{j=1}^k n_j(\bar{x}_j - \bar{x})^2 = 21.563144, e che \mathscr{D}^2_\text{en} = \sum_{j=1}^k d^2_j = 52.207824. Da ciò si conclude che \mathscr{D} = \mathscr{D}^2_\text{tr} + \mathscr{D}^2_\text{en} = 73.770968. Un indice di dipendenza in media è quindi dato da:
\eta^2 = \frac{\mathscr{D}^2_\text{tr}}{\mathscr{D}} = 0.292299.
Da questo si deduce una discreta dipendenza in media. Nota: questo valore è identico a \chi^2_\text{norm}, nonostante sia stato ottenuto attraverso una procedura completamente diversa. Non si tratta di una coincidenza, anche se la dimostrazione di questo fatto non è immediata. In presenza di variabili binarie, infatti, vale che \eta^2 = \chi^2_\text{norm} (!).
Problema 3
Siano x_1,\dots,x_n ed y_1,\dots,y_n due insiemi di dati e siano w_1,\dots,w_n dei dati trasformati tali che w_i = x_i + y_i, per i=1,\dots,n.
In quali circostanze la relazione \text{var}(w) = \text{var}(x) + \text{var}(y) risulta verificata?
Si dimostri la seguente disuguaglianza: |\text{cov}(x, y)| \le \text{sqm}(x)\text{sqm}(y).
Si tratta di argomenti trattati a lezione, per cui si rimanda alle slides e/o al libro di testo. Per quel che riguarda il primo punto, la relazione è verificata se \text{cov}(x, y) = 0.