Statistica I

Esercizi 1: distribuzioni di frequenza

Author
Affiliation

Tommaso Rigon

Università degli Studi di Milano-Bicocca

Homepage

Le soluzioni di alcuni esercizi sono state gentilmente fornite dal tutor di Statistica I dell’A.A. 2021/2022, Alex Alborghetti, che ringrazio. Le soluzioni sono state quindi riviste dal docente, che si assume le responsabilità di eventuali sviste ed errori.

Esercizio A (Peso pacchetti di burro)

Il controllo sul peso (in grammi) di n = 71 pacchetti di burro ha fornito la seguente distribuzione di frequenza cumulata.

c_j (grammi) (249,250] (250, 251] (251, 252] (252, 253] (253, 254] (254 , 255]
N_j 0 15 42 60 70 71

  1. Si dica qual è l’unità statistica e la tipologia della variabile considerata.

  2. Trovare le frequenze assolute n_1,\dots,n_k e relative f_1,\dots,f_k.

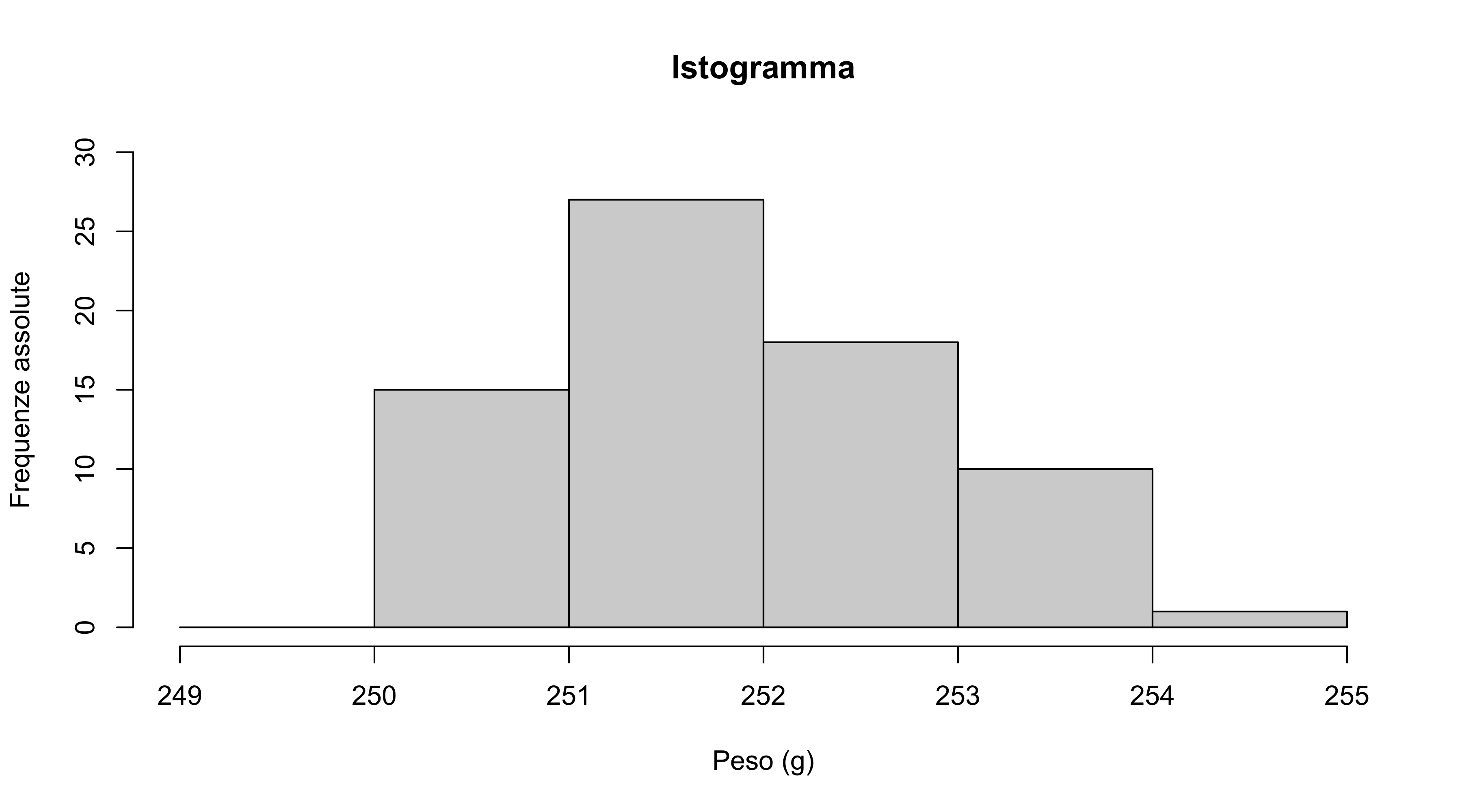
  3. Rappresentare graficamente il fenomeno tramite un istogramma.

  4. Quanti sono i pacchetti di burro che pesano meno di 252g? Quanti quelli che hanno un peso compreso nell’intervallo (251, 252]?

L’unità statistica considerata è il pacchetto di burro, mentre la variabile considerata è di tipo quantitativo continuo, poiché il peso di ciascun pacchetto può assumere valori in \mathbb{R}^+. I dati sono suddivisi in sei classi di ampiezza pari a 1 g.

Ricordando la definizione della generica frequenza cumulata:

N_j = n_1 + \dots + n_j = \sum_{j'=1}^j n_{j'}, \quad \text{con} \; j = 1, \dots, k, si può quindi notare che la j-esima frequenza assoluta n_j è ottenibile come scarto tra N_j ed N_{j-1}, ovvero: N_j - N_{j-1} = n_1 + \dots + n_{j-1} + n_j - (n_1 + \dots + n_{j-1}) = n_j. Applicando questa formula si può quindi ricavare la seguente tabella:

Classe Freq. cumulata Freq. assoluta
(249, 250] 0 0
(250, 251] 15 15
(251, 252] 42 42 - 15 = 27
(252, 253] 60 60 - 42 = 18
(253, 254] 70 70 - 60 = 10
(254, 255] 71 71 - 70 = 1

Le frequenze relative, invece, si ottengono semplicemente rapportando le frequenze assolute alla numerosità campionaria, in questo caso pari ad n = 71.

Classe Freq. cumulata Freq. relativa
(249, 250] 0 0
(250, 251] 15 15/71 = 0.211
(251, 252] 42 27/71 = 0.380
(252, 253] 60 18/71 = 0.254
(253, 254] 70 10/71 = 0.141
(254, 255] 71 1/71 = 0.014

I pacchetti di burro che pesano al più 252 g sono F(252) = 42.

Esercizio B (Errori di stampa)

Durante la correzione delle bozze di un libro di 280 pagine si è riscontrata la seguente distribuzione degli errori di stampa per pagina:

Numero di errori Frequenze assolute
0 112
1 88
2 44
3 18
4 10
5 8

  1. Qual è l’unità statistica?

  2. Di quale tipologia di variabile si tratta?

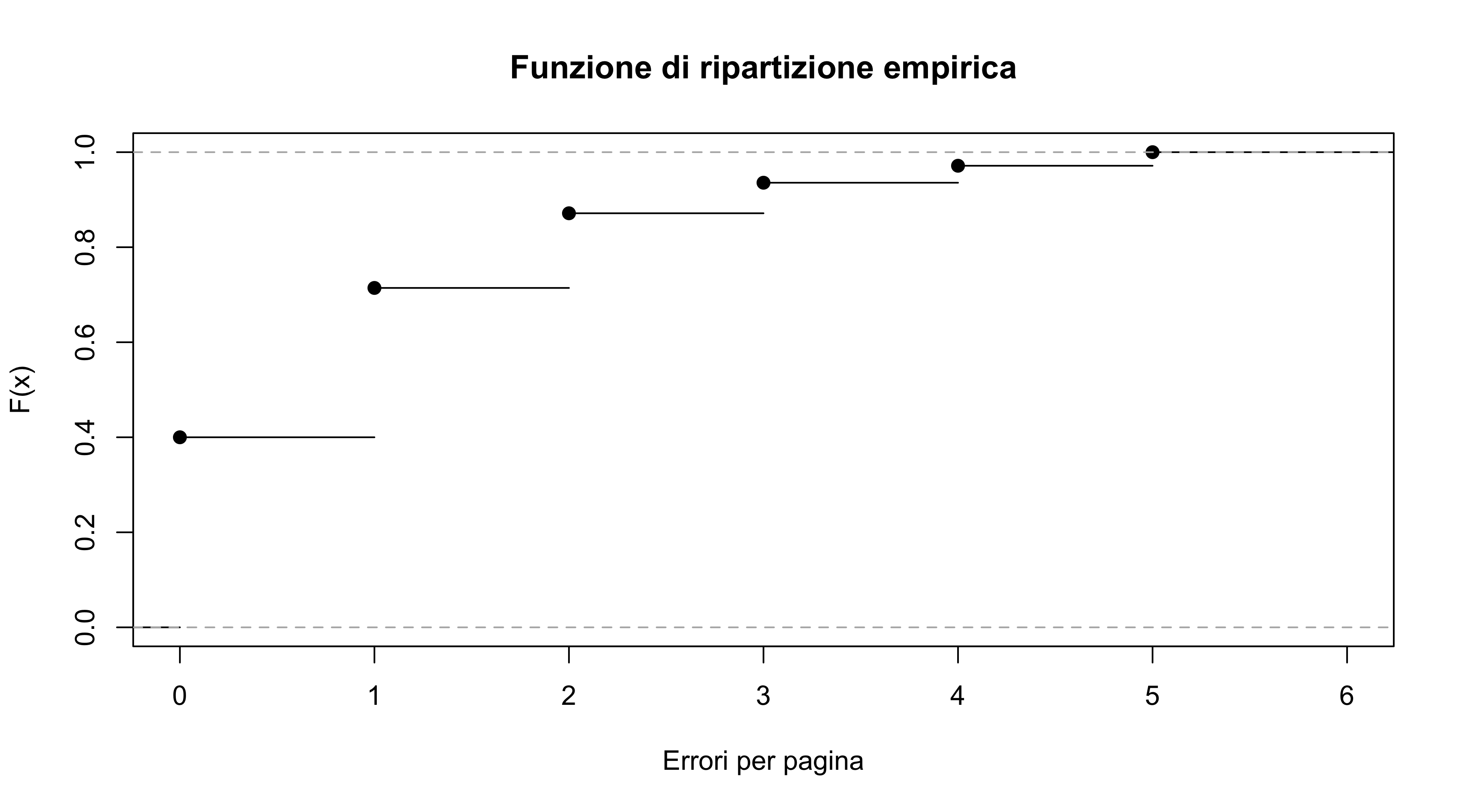
  3. Calcolare e disegnare la funzione di ripartizione.

  4. Qual è la proporzione di pagine con meno di 3 errori? Quanto vale F(3)?

L’unità statistica è la pagina del libro. Il numero di errori di stampa per pagina è una variabile quantitativa discreta, poiché assume valori interi.

Ricordando la definizione di funzione di ripartizione empirica: F(x) = \frac{1}{n} \sum_{i=1}^n \mathbb{I}(x_i \leq x), possiamo quindi ottenere la seguente tabella:

Valore F(x)
0 112/280 = 0.4
1 200/280 = 0.714
2 244/280 = 0.871
3 262/280 = 0.936
4 272/280 = 0.971
5 1

La cui rappresentazione grafica è data da:

I risultati sono arrotondati a tre cifre decimali. La proporzione di pagine con meno di tre errori è F(2) = 0.871, mentre F(3) = 0.936, come visibile dalla tabella precedente.

Esercizio C (Titolo di studio)

Ai dipendenti di una piccola azienda è stato chiesto di precisare il loro titolo di studio. I risultati relativi a n=22 dipendenti sono i seguenti:

L, E, E, E, I, E, I, S, L, E, S, I, N, E, N, S, S, I, E, I, I, S

in cui: N = nessun titolo di studio, E = licenza elementare, I = licenza media inferiore, S = licenza media superiore, e L = laurea.

  1. Qual è l’unità statistica? Di quale tipologia di variabile si tratta?

  2. Organizzare i dati in una tabella.

  3. Calcolare le frequenze relative.

  4. Si calcoli la percentuale di dipendenti aventi la licenza media o un titolo superiore.

Esercizio D (Cicchitelli, esercizio 2.4)

Quella che segue è una distribuzione di frequenze di famiglie italiane secondo il numero di componenti (dati Istat; frequenze espresse in migliaia)

Numero di componenti 1 2 3 4 5 6 o più
Numero di famiglie (in migliaia) 5428 5905 4136 1266 369 71

  1. Si riscriva la tabella riportando accanto alle frequenze assolute quelle relative. Sulla base di questo, poi, si faccia un commento sulla struttura della famiglia in Italia

  2. Si determinino le frequenze cumulate relative e si commentino i risultati.

Esercizio E

Si considerino le funzioni di ripartizione relative alle variabili x ed y

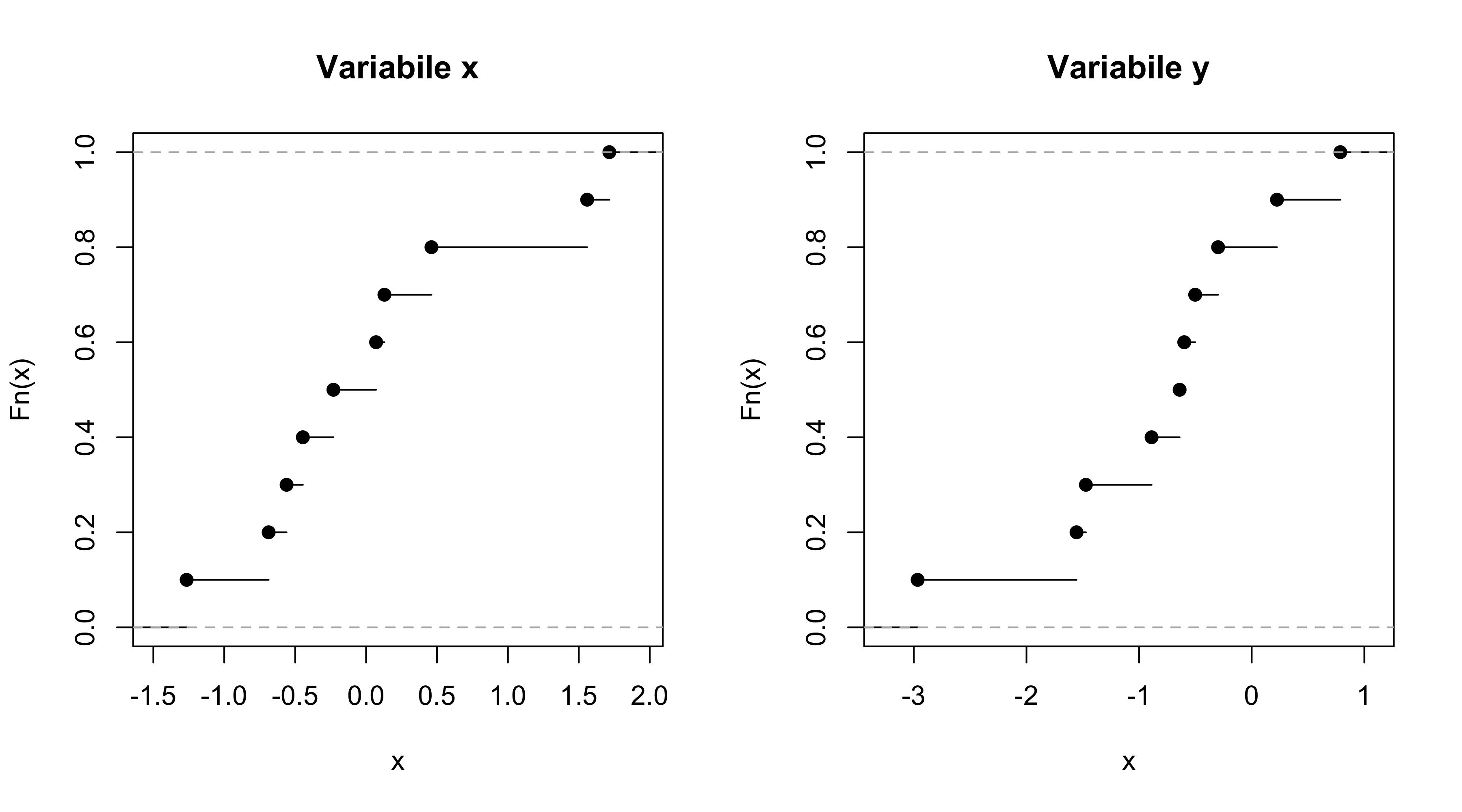
  1. Quale variabile assume valori tendenzialmente maggiori?

  2. Sulla base del grafico, quanto vale approssimativamente F_x(0), dove F_x(\cdot) è la funzione di ripartizione della variabile x? Quanto vale F_x(2)?

  3. Sulla base del grafico, quanto valgono il minimo ed il massimo della variabile y?

  4. Si dica quale dei seguenti vettori sono i dati x e quale invece sono i dati y (si ignori il simbolo [1]). Si ottengano quindi i valori precisi delle quantità calcolate nei punti precedenti.

##  [1]  0.22 -0.64 -0.60 -0.89 -1.56  0.79 -0.50 -2.97 -0.30 -1.47
##  [1] -0.56 -0.23  1.56  0.07  0.13  1.72  0.46 -1.27 -0.69 -0.45

La variabile y assume valori tendenzialmente minori della variabile x, dato che dal grafico sembra appartenere all’intervallo (-1.3, 1.5) circa, mentre la variabile y appartiene all’intervallo (-3, 0.8) circa.

A giudicare dal grafico, vale approssimativamente che F_x(0) = 0.6, mentre F_x (2) = 1, dove F_x(\cdot) rappresenta la funzione di ripartizione empirica della variabile x.

Come già osservato in precedenza, y sembra appartenere all’intervallo (-3, 0.8), pertanto: y = (0.22,\:-0.64,\: -0.60,\: -0.89,\: -1.56,\: 0.79,\: -0.50,\: -2.97,\: -0.30,\: -1.47) e x = (-0.56,\: -0.23,\: 1.56,\: 0.07,\: 0.13,\: 1.72,\: 0.46,\: -1.27,\: -0.69,\: -0.45), Inoltre, si ottiene che: F_x(0) = \frac{1}{10} \sum_{i=1}^{10} \mathbb{I}(x_i \leq 0) = 0.5, \qquad F_x(2) = \frac{1}{10} \sum_{i=1}^{10} \mathbb{I}(x_i \leq 2) = 1. I valori del massimo e del minimo di y sono invece i seguenti: \min(y) = -2.97, \quad \max(y) = 0.79.