Statistica I

Esercizi 2: indici di posizione

Autore/Autrice
Affiliazione

Tommaso Rigon

Università degli Studi di Milano-Bicocca

Homepage

Alcune delle seguenti soluzioni sono state gentilmente fornite dal tutor di Statistica I dell’A.A. 2021/2022, Alex Alborghetti, che ringrazio. Le soluzioni sono state quindi riviste dal docente, che si assume le responsabilità di eventuali sviste ed errori.

Esercizio A (Velocità della luce, continuazione)

Si faccia riferimento ai dati trasformati y_1,\dots,y_{66} dell’Esercitazione 1, riguardanti la la velocità della luce.

Domande

  1. Si calcoli la media e la mediana dei dati. Si commentino i risultati.
  2. Si escluda il valore anomalo (-44) dall’analisi e si calcolino nuovamente media e mediana. Si commenti.

I risultati che seguono non costituiscono la soluzione completa dato che i vari passaggi sono stati omessi.

Media e mediana

La media dei dati trasformati è circa 26.21 mentre la mediana è 27.

Media e mediana dati trasformati

La media dei dati trasformati, escluso il valore anomalo -44, è pari a 27.29 mentre la mediana è 27.

Commento

Il valore anomalo influenza sensibilmente il valore della media aritmetica. Viceversa, la mediana rimane invariata.

Esercizio B (Gran premio del Canada)

Il Gran premio del Canada viene interrotto per la pioggia dopo 42 giri, quando il pilota A era in terza posizione, con una velocità media di 204 km/h. I restanti 21 giri vengono percorsi da dal pilota A ad una media di 126 km/h. Il circuito misura 5 km. Al termine si sommano i tempi delle due frazioni di gara e il pilota A risulta il vincitore.

Domande

  1. Calcolare la velocità media del pilota A.

  2. Calcolare la durata delle due frazioni di gara e quella complessiva.

In totale ci sono n = 63 \times 5 = 315 km da percorrere, di cui 42 \times 5 = 210 nella prima frazione di gara e 21 \times 5 = 105 nella seconda. La velocità media complessiva si ottiene tramite una media armonica ponderata, ovvero

\mathbb{A} = \frac{315}{210/204 + 105/126}= \frac{63}{42/204 + 21/126} = 169.1053. Le durate delle due frazioni di gara t_1, t_2 sono pari a (tempo) = (distanza) / (velocità) e pertanto si ottiene che

t_1 = 210 / 204 = 1.0294 \text{h}, \qquad t_2 = 105 / 126 = 0.8\bar{3} \text{h}, per un totale di t_1 + t_2 = 1.8627 ore.

Esercizio C (Trasformazioni dei dati)

Per le osservazioni x_1,\dots,x_{11}, i cui valori sono (−4, 5, 3, 1, −1, 3, −1, 1, 0, 3, 2), si calcolino media e mediana.

Inoltre, si dica quali sono mediana e media delle osservazioni trasformate y_1,\dots,y_{11} che si ottengono trasformando i dati di partenza secondo le funzioni

y_i = f_1(x_i)=e^{x_i}, \quad i=1,\dots,11. y_i = f_2(x_i) = x_i + 4, \qquad i=1,\dots,11.

y_i = f_3(x_i) = -3 x_i + 1,\qquad i=1,\dots,11. y_i = f_4(x_i) = x_i^2, \qquad i =1,\dots,11.

Nota

Se possibile, si eviti di calcolare i valori y_1,\dots,y_n.

È dato il vettore di osservazioni:

x = (-4,5,3,1,-1,3,-1,1,0,3,2) Ricordando la definizione di media aritmetica, si ottiene quindi che: \bar{x} = \frac{1}{n}\sum_{i=1}^nx_i = \frac{-4+5+3+\cdots + 2}{11} = 1.091

Si trova facilmente dalla definizione che \text{Me}(x) = x_{(6)} = 1. Sia f(x) una trasformazione monotona dei dati di partenza, allora \text{Me}(f(x)) = f(\text{Me}(x)).

La media, invece, gode della proprietà di linearità, tale per cui \bar{y} = a + b\bar{x}. Grazie a queste due proprietà, si possono ricavare i seguenti valori:

y \text{Me}(y) \bar{y}
e^x e^{\text{Me}(x)} = e^1 = e -
x+4 \text{Me}(x) + 4 = 5 \bar{x}+4 = 5.091
-3x+1 -3 \text{Me}(x) +1=-2 -3\bar{x}+1 = -2.273
x^2 - -

I tre spazi vuoti della tabella, invece, vanno necessariamente completati trasformando manualmente i dati e calcolando gli indici richiesti.

Si trova che \bar{y} = n^{-1}\sum_{i=1}^n e^{x_i} = 20.295, \text{Me}(x^2) = 4 e \bar{y} = n^{-1}\sum_{i=1}^n x_i^2 = 6.909. I risultati sono stati arrotondati a tre cifre decimali.

Esercizio D (Età ed altezza)

Di un gruppo di n = 100 ragazzi appartenenti ad una società sportiva si hanno le seguenti informazioni sull’età (in anni compiuti) e sulla statura (in cm). Sapendo che la media della statura relativa ai 100 ragazzi è di 178 cm, si determini:

  1. La media della statura per i n_2 = 40 ragazzi di 17 anni.

  2. La media dell’età.

È inoltre noto che:

Età Numerosità (n_j) Media statura
16 40 175
17 40 (ignota)
18 20 180

Esercizio E (Ditta di trasporti)

Una ditta di trasporti rifornisce con uguale periodicità cinque negozi posti rispettivamente ai chilometri 50, 89, 134, 198, 530 di una stessa strada.

Avendo deciso di costruire un magazzino sulla strada medesima, la ditta vuole stabilirne la posizione (ovvero il chilometro della strada) in modo da minimizzare la distanza percorsa per rifornire i cinque negozi.

Nota

Un camion rifornisce un negozio e poi deve tornare al magazzino.

La distanza di un negozio dal magazzino può essere espressa come lo scarto |x_i - a|km, dove x_i è il chilometro al quale si trova il negozio, mentre a è il chilometro al quale si trova il magazzino.

Si deve individuare quel valore a tale per cui il doppio (andata e ritorno) della somma di questi scarti viene minimizzata. Il valore a deve, pertanto, corrispondere alla mediana, che vale 134.

La distanza totale percorsa per rifornire tutti e cinque i negozi è pari a 1178km. Se avessimo posizionato il magazzino sul chilometro pari alla media, che vale 200.2km, avremmo dovuto percorrere 1319.2km.

Esercizio F (continuazione pacchetti di burro)

Il controllo sul peso (in grammi) di n = 71 pacchetti di burro ha fornito la seguente distribuzione di frequenza cumulata.

Peso c_j (0,250] (250, 251] (251, 252] (252, 253] (253, 254] (254 , 255]
Frequenza cumulata 0 15 42 60 70 71

Effettuando, se necessarie, le dovute approssimazioni:

  1. Si calcolino media e mediana del peso dei pacchetti di burro.

  2. Si calcoli il primo ed il terzo quartile.

Una tipica approssimazione della media, quando i dati sono suddivisi in classi, è la seguente: \bar{x} \approx \frac{1}{n} \sum_{j=1}^k n_jm_j, dove m_j è il punto centrale del j-esimo intervallo ed n_j è la sua frequenza assoluta.

Classe Freq. cumulata Freq. Assoluta
(249, 250] 0 0
(250, 251] 15 15
(251, 252] 42 42 - 15 = 27
(252, 253] 60 60 - 42 = 18
(253, 254] 70 70 - 60 = 10
(254, 255] 71 71 - 70 = 1

Quindi, possiamo calcolare la media come:

\bar{x} \approx \frac{0\cdot249.5+15\cdot250.5+27\cdot251.5+18\cdot252.5+10\cdot253.5+1\cdot254.5}{71} = 251.866.

Invece, una comune approssimazione della mediana quando i dati sono suddivisi in classi è data da: \text{Me}(x) \approx a_{j-1} + (a_j - a_{j-1})\frac{1/2 - F(a_{j-1})}{F(a_{j})-F(a_{j-1})},

dove (a_{j-1}, a_{j}] è la classe alla quale la mediana appartiene ed F(\cdot) è la funzione di ripartizione empirica.

Nel nostro caso, la mediana, ovvero l’osservazione x_{(36)}, appartiene all’intervallo (251,252]. Sappiamo, inoltre, che F(252) = 42/71 = 0.592 e F(251) = 15/71 = 0.211. Sostituendo tutti i valori nella formula, si ricava: \text{Me}(x) \approx 251.759.

Un’approssimazione del primo quartile, quando i dati sono suddivisi in classi, è invece: Q_{0.25} \approx a_{j-1} + (a_j - a_{j-1})\frac{0.25 - F(a_{j-1})}{F(a_{j})-F(a_{j-1})}, dove (a_{j-1}, a_{j}] è la classe alla quale il primo quartile appartiene. Poiché il primo quartile apartiene all’intervallo (251,252], dato che F(252) = 0.592 e F(251) = 0.211, sostituendo questi valori nella formula troviamo che Q_{0.25} \approx 251.102.

L’approssimazione del terzo quartile quando i dati sono suddivisi si ottiene invece tramite la formula: Q_{0.75} \approx a_{j-1} + (a_j - a_{j-1})\frac{0.75 - F(a_{j-1})}{F(a_{j})-F(a_{j-1})}, dove (a_{j-1}, a_{j}] è la classe alla quale il terzo quartile appartiene.

Poiché il terzo quartile appartiene alla classe (252,253] dato che F(252) = 0.592 e F(253) = 60/71 = 0.845, sostituendo nella formula troviamo che Q_{0.75} \approx 252.625.

Esercizio G (Soddisfazione dipendenti)

Ai dipendenti di un’azienda è stato chiesto di indicare il grado di soddisfazione (1 = scarsa; 10 = ottima) riguardo alla qualità del cibo distribuito dalla mensa aziendale. I dati sono i seguenti:

Giudizio 1 2 3 4 5 6 7 8 9 10
Frequenza assoluta 35 44 52 56 48 69 62 16 16 2

  1. Costruire la funzione di ripartizione empirica e commentare i risultati.

  2. Calcolare il valore medio, mediano, il primo e il terzo quartile. Commentare i risultati.

  3. A quale percentile corrisponde il valore 7 del grado di soddisfazione? Spiegare il risultato.

  4. I dipendenti risultano concordi nella valutazione della mensa? Sono contenti o scontenti? Cosa suggerireste ai responsabili della mensa?

☠️ - Esercizio H

In un’azienda industriale si hanno 5 linee diverse di produzione. Per ogni produzione si sono rilevati i dati seguenti

Linea di produzione A B C D E
Numero di pezzi (x) 5 10 20 10 4

  1. Si calcoli il numero medio di pezzi prodotti tale da lasciare immutato il consumo totale di energia z, nell’ipotesi che tra consumo energetico e numero di pezzi prodotti sussista la relazione: z = k + h(x + 0.1 x^2), dove k e h sono due valori costanti non noti. Suggerimento: si utilizzi l’approcco di Chisini.

  2. Si svolga ora l’esercizio ipotizzando la relazione z = k + hx, dove k e h sono due valori costanti non noti.

Esercizio I

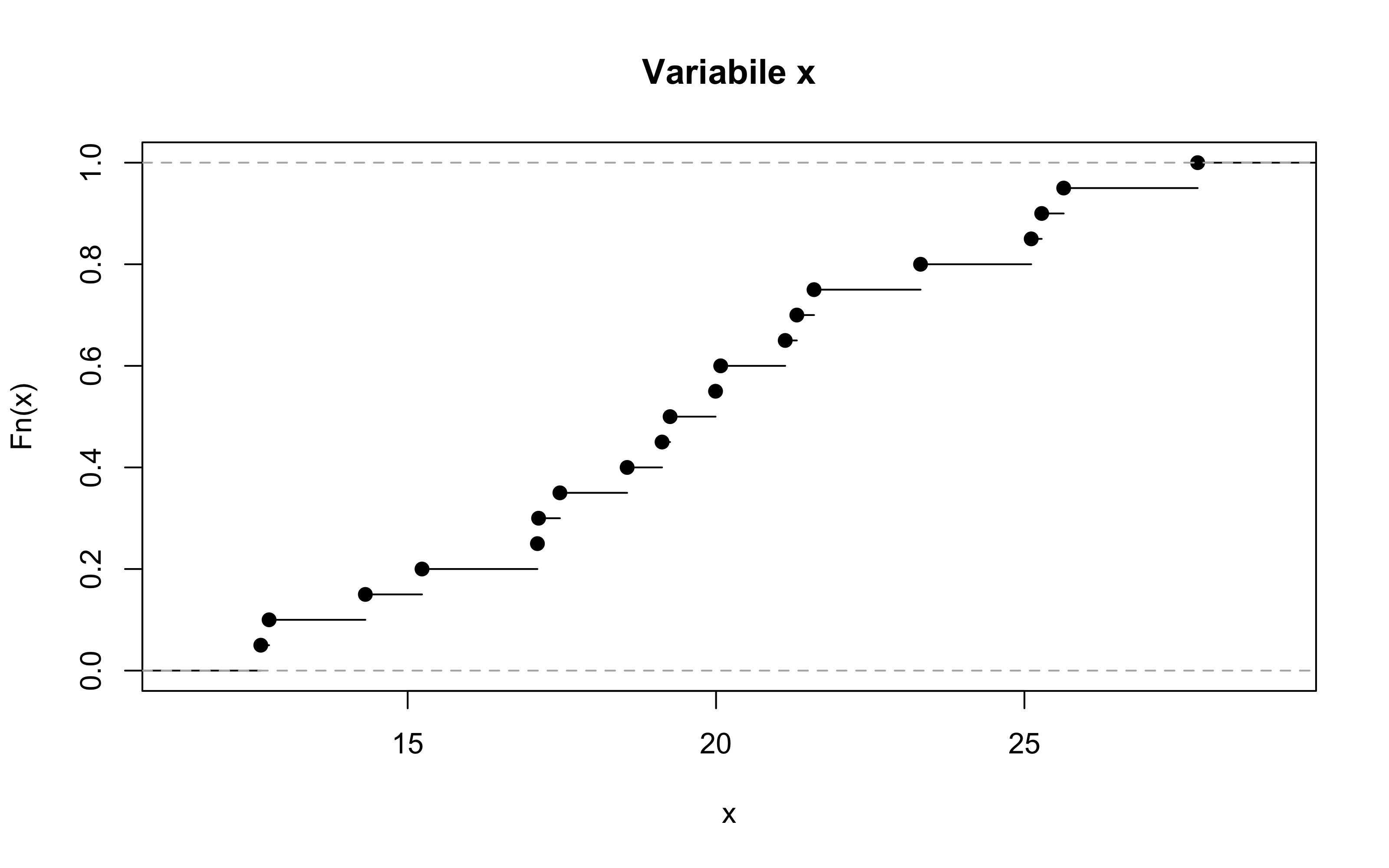
Si consideri la seguente funzione di ripartizione della variabile x, con n = 20.

  1. Quanto vale (approssimativamente) la mediana della variabile x?

  2. Quanto valgono (approssimativamente) il primo ed il terzo quartile?

La mediana della variabile x vale circa 17. Il primo quartile vale circa 16, il terzo 22.