Statistica I
Esercizi 3: variabilità, istogrammi, boxplot, simmetria, curtosi
Homepage
Le soluzioni di alcuni esercizi sono state gentilmente fornite dal tutor di Statistica I dell’A.A. 2021/2022, Alex Alborghetti, che ringrazio. Le soluzioni sono state quindi riviste dal docente, che si assume le responsabilità di eventuali sviste ed errori.
Esercizio A
Si considerino i seguenti tre insiemi di n = 10 dati raccolti sulla medesima variabile in tre situazioni diverse: x = (−1.65, −5.74, −0.84, −4.50, 12.90, 0.84, −4.73, 7.89, 10.72, 4.40), y = (−5.34,−6.26,3.80,−2.15,−1.72,−7.35,6.84,5.92,1.72,7.76), z = (7.05, −0.43, −10.21, −5.44, −6.75, −12.33, 13.76, 21.51, 0.43, 6.14).
Si confrontino le variabilità, la simmetria e la curtosi di questi insiemi dapprima con uno strumento grafico e, successivamente, con appositi indici.
Sono presenti outlier nei precedenti insiemi?
Esercizio B (Giorni di ferie)
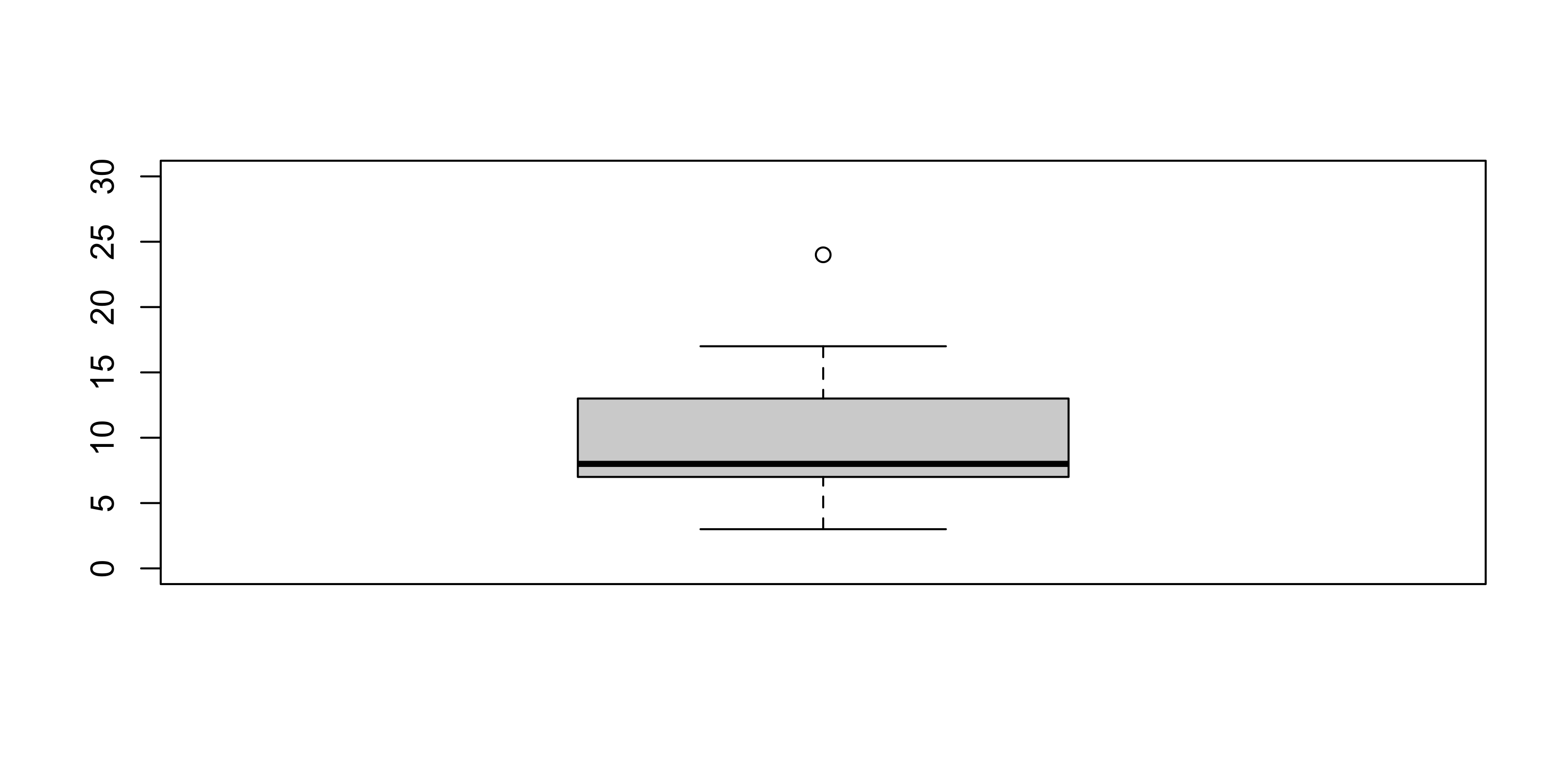
Il numero di giorni di ferie richiesti per il mese di giugno 2019 in un campione di n = 16 lavoratori è rappresentato nella seguente tabella
| Modalità c_j | 3 | 7 | 8 | 11 | 15 | 17 | 24 |
|---|---|---|---|---|---|---|---|
| Frequenze assolute n_j | 2 | 4 | 5 | 1 | 2 | 1 | 1 |
Rappresentare graficamente la funzione di ripartizione empirica.
Calcolare la mediana e i quartili.
Sono presenti outlier? Quindi, disegnare un boxplot.
Determinare media aritmetica.
Calcolare il campo di variazione, la differenza interquartile e lo scarto quadratico medio.
Schema della soluzione
Viene riportata la tabella con le frequenze relative cumulate:
| Modalità | Freq. assoluta cumulata | Freq. relativa cumulata |
|---|---|---|
| 3 | 2 | 0.125 |
| 7 | 6 | 0.375 |
| 8 | 11 | 0.688 |
| 11 | 12 | 0.750 |
| 15 | 14 | 0.875 |
| 17 | 15 | 0.938 |
| 24 | 16 | 1 |
Dalla tabella precedente, si ottiene \text{Me} = 8, \mathcal{Q}_{0.25} = 7 e \mathcal{Q}_{0.75} = 11, che sono i più piccoli valori che, rispettivamente, lasciano alla propria sinistra almeno il 50\%, 25\% e il 75\% dei dati.
Costruiamo il boxplot. Abbiamo già i quartili, dobbiamo trovare i “baffi”. Il baffo inferiore è definito come:
\max\{\min(x), \mathcal{Q}_{0.25}- 1.5 (\mathcal{Q}_{0.75} - \mathcal{Q}_{0.25})\} = \max\{3, 1\} = 3, quello superiore è definito come:
\min\{\max(x), \mathcal{Q}_{0.75} + 1.5 (\mathcal{Q}_{0.75} - \mathcal{Q}_{0.25})\} = \min\{24, 17\} = 17 Tutti i punti al di fuori dell’intervallo [3, 17], dunque, sono considerati anomali. Nel nostro caso, solamente il valore x_{(16)} = 24 è anomalo.
La media aritmetica vale:
\bar{x} = \frac{2 \times 3 + 4 \times 7 + \dots}{16} = 9.75.
Il campo di variazione è lo scarto tra il valore massimo e il valore minimo, in questo caso 24-3 = 21. La differenza interquartile vale \mathcal{Q}_{0.75} - \mathcal{Q}_{0.25} = 4.
Lo scarto quadratico medio è per definizione pari a \sigma = \sqrt{\sigma^2}. Possiamo riscrivere il termine \sigma^2 come:
\begin{split} \sigma^2 =& \frac{1}{n} \sum_{i=1}^n(x_i-\bar{x})^2 = \frac{1}{n} \sum_{i=1}^n (x_i^2 - 2x_i\bar{x} + \bar{x}^2)\\ &=\frac{1}{n} \sum_{i=1}^nx_i^2 -\frac{2}{n} \bar{x}\sum_{i=1}^n x_i + \bar{x}^2 \\ & =\frac{1}{n} \sum_{i=1}^nx_i^2 - \bar{x}^2 \\ &=\frac{2\cdot3^2+4\cdot7^2+\dots}{16} - 9.75^2 = 28.0625. \end{split}
Allora \sigma = \sqrt{28.0625} = 5.297.
Esercizio C (Gravidanze in Italia)
Nel 1975 in Italia il numero di parti legittimi per età della madre al parto è stato il seguente:
| Età della madre | Numero nati |
|---|---|
| (9, 14] | 489 |
| (14, 20] | 94921 |
| (20, 24] | 200255 |
| (24, 29] | 274779 |
| (29, 34] | 144282 |
| (34, 44] | 99238 |
| (44, 55] | 1747 |
Si dica qual è l’unità statistica e qual è la variabile considerata.
Di che tipo di variabile si tratta?
Rappresentare graficamente il fenomeno. Attenzione: le classi non hanno dimensione uguale.
Calcolare la percentuale dei nati per fasce d’età della madre.
Esercizio D (Voto esame di maturità)
Per n = 56 studenti si è rilevata la variabile voto all’esame di maturità. Il voto medio rilevato è pari a 76 e la varianza pari a 25.
Se si osserva un ulteriore studente che ha riportato un voto pari a 90. Qual è il nuovo voto medio?
Nella stessa ipotesi, come cambia la varianza?
Se lo studente che si aggiunge ha riportato un voto pari a 76 come cambiano le risposte ai quesiti precedenti?
☠️ - Esercizio E
Sia x una variabile binaria, ovvero una variable che può assumere solo due modalità (0 e 1). La frequenza relativa associata al valore 1 è f_1 mentre quella associata al valore 0 è f_0 = 1 - f_1.
Si calcoli la varianza della variabile x in funzione di f_1, ovvero \text{var}(x). Si supponga quindi che f_1 = 0.4 e si dica quanto vale la varianza in questo caso particolare.
Si disegni il grafico di \text{var}(x) in funzione di f_1. Si trovi quindi il valore di f_1 che rende massima \text{var}(x).
☠️ - Esercizio F
Il peso (in kg) degli individui maschi adulti di una certa popolazione si distribuisce con media \bar{x} = 70 e deviazione standard \sigma = 15. Supponendo di non aver accesso ai dati completi, cosa è possibile dire riguardo alla frequenza relativa di individui appartenenti alle seguenti classi?
- Frequenza relativa della classe di peso [50, 90].
- Frequenza relativa della classe di peso [55, 85].
- (Difficile) Frequenza relativa della classe di peso [50, 100].
Si commentino i risultati.
Suggerimento. Si faccia uso della disuguaglianza di Chebyshev. Per quel che riguarda il terzo punto, si noti che [50,90] \subset [50,100].
Esercizio G
I dati x_1,\dots,x_n e y_1,\dots,y_n sono rappresentati negli istogrammi seguenti
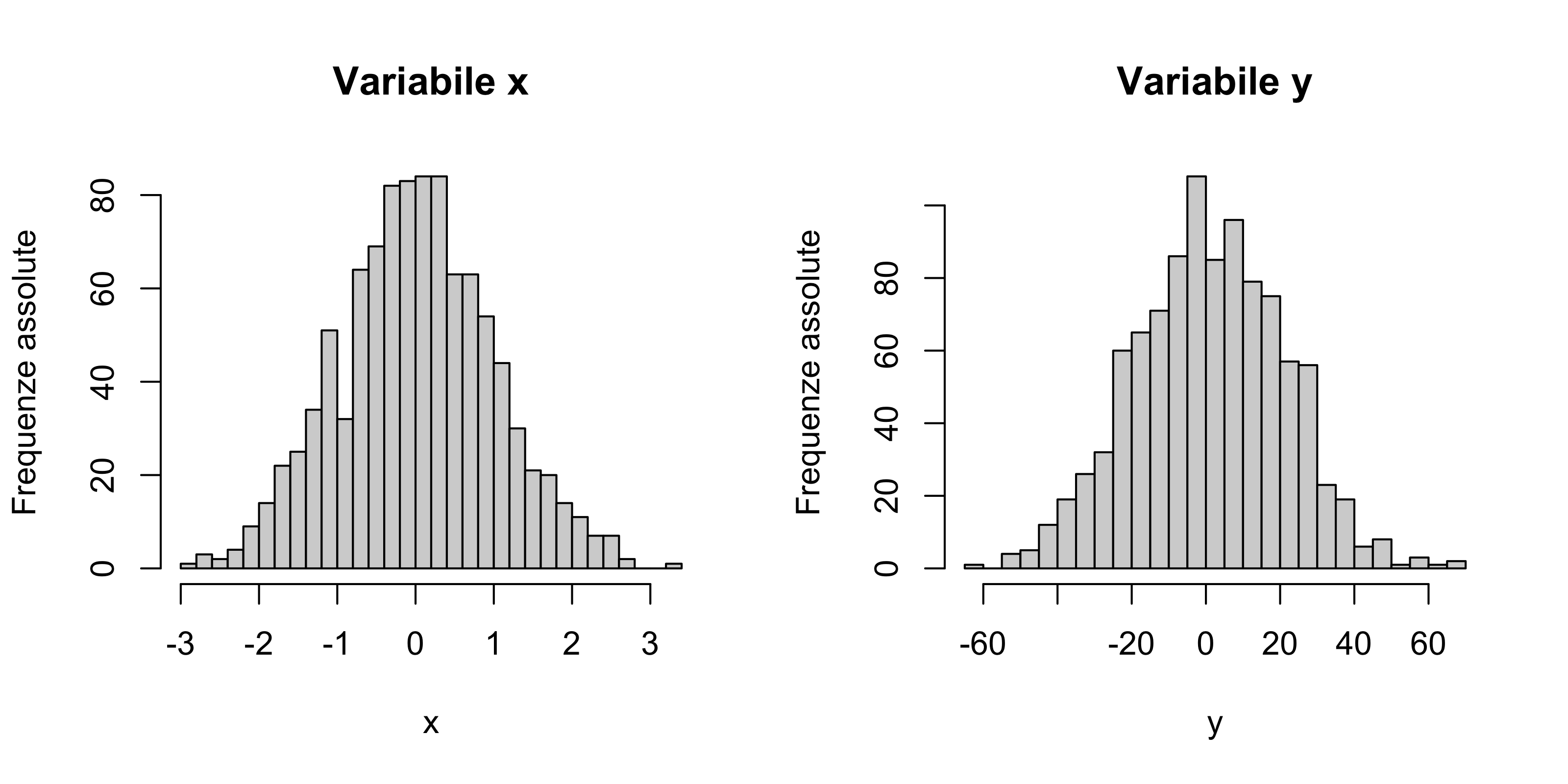
Quale delle due variabili presenta la maggiore variabilità?
A giudicare dal grafico, quando vale (approssimativamente) l’indice di asimmetria di Pearson? E quello di Bowley?
Esercizio H (Altezza delle persone)
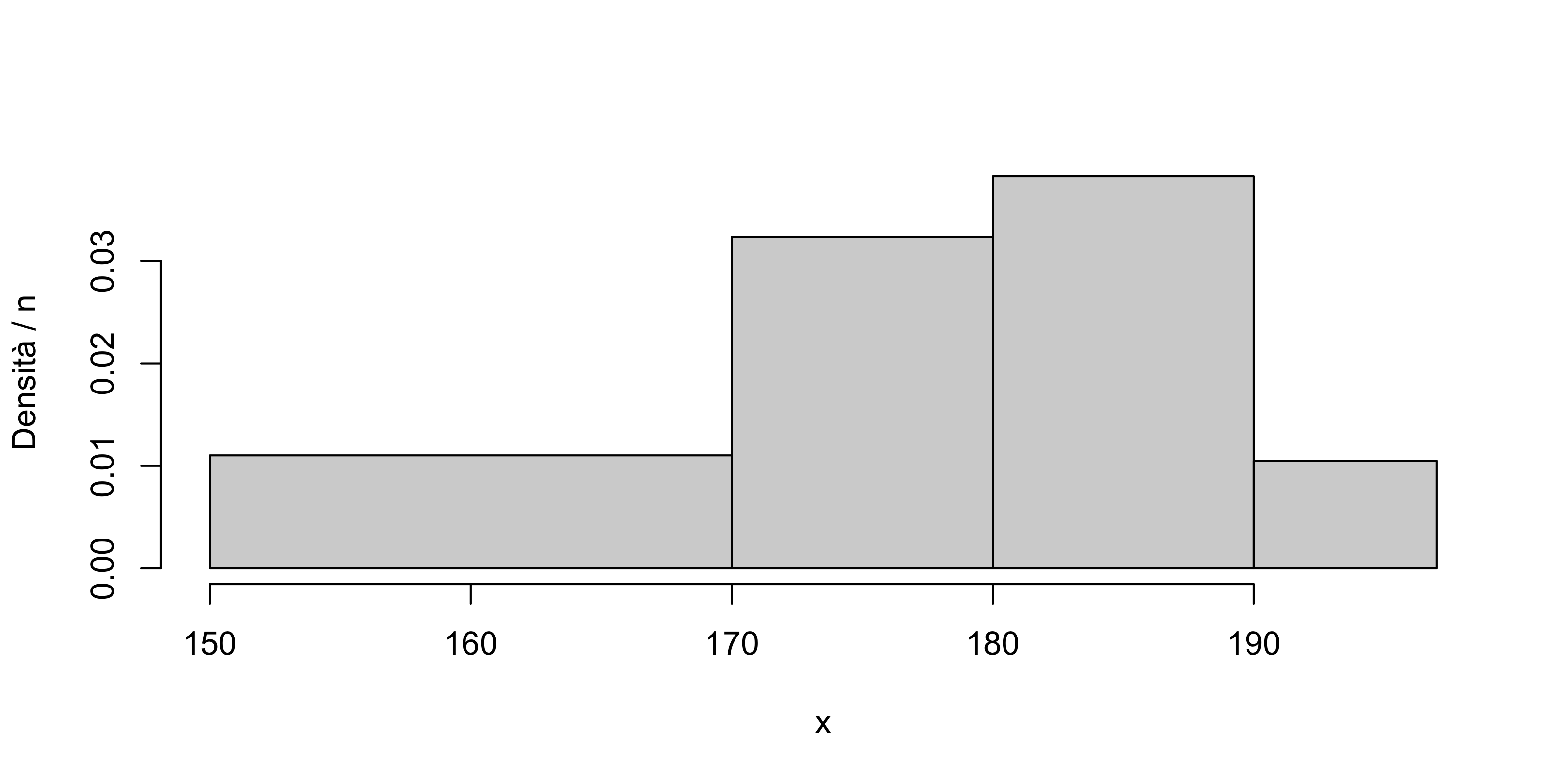
Rilevando in centrimetri la statura di n = 136 persone, si sono contate 30 persone con statura compresa tra i 150 e 170cm; 44 con statura tra 170 e 180; 52 tra 180 e 190 e 10 tra 190 e 197, che è la statura massima rilevata.
Si rappresentino i dati con un istogramma.
Schema della soluzione
Supponendo che le classi siano chiuse a destra, possiamo rappresentare i dati nella seguente tabella:
| Classi di statura | Frequenza assoluta | Ampiezza della classe | Densità di frequenza | Altezza rettangoli |
|---|---|---|---|---|
| (150, 170] | 30 | 20 | 1.5 | 0.011 |
| (170, 180] | 44 | 10 | 4.4 | 0.032 |
| (180,190] | 52 | 10 | 5.2 | 0.038 |
| (190,197] | 10 | 7 | 1.429 | 0.010 |
Esercizio I (Moscerini della frutta)
Un gruppo di ricercatori sta valutando la tossicità su D. melanogaster (moscerini della frutta) di un composto molecolare. I moscerini vengono divisi casualmente in 10 gruppi e vengono trattati col composto. Dopo 1 giorno si registra la percentuale di moscerini non sopravvissuti per l’eccessiva tossicità.
| Gruppo | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
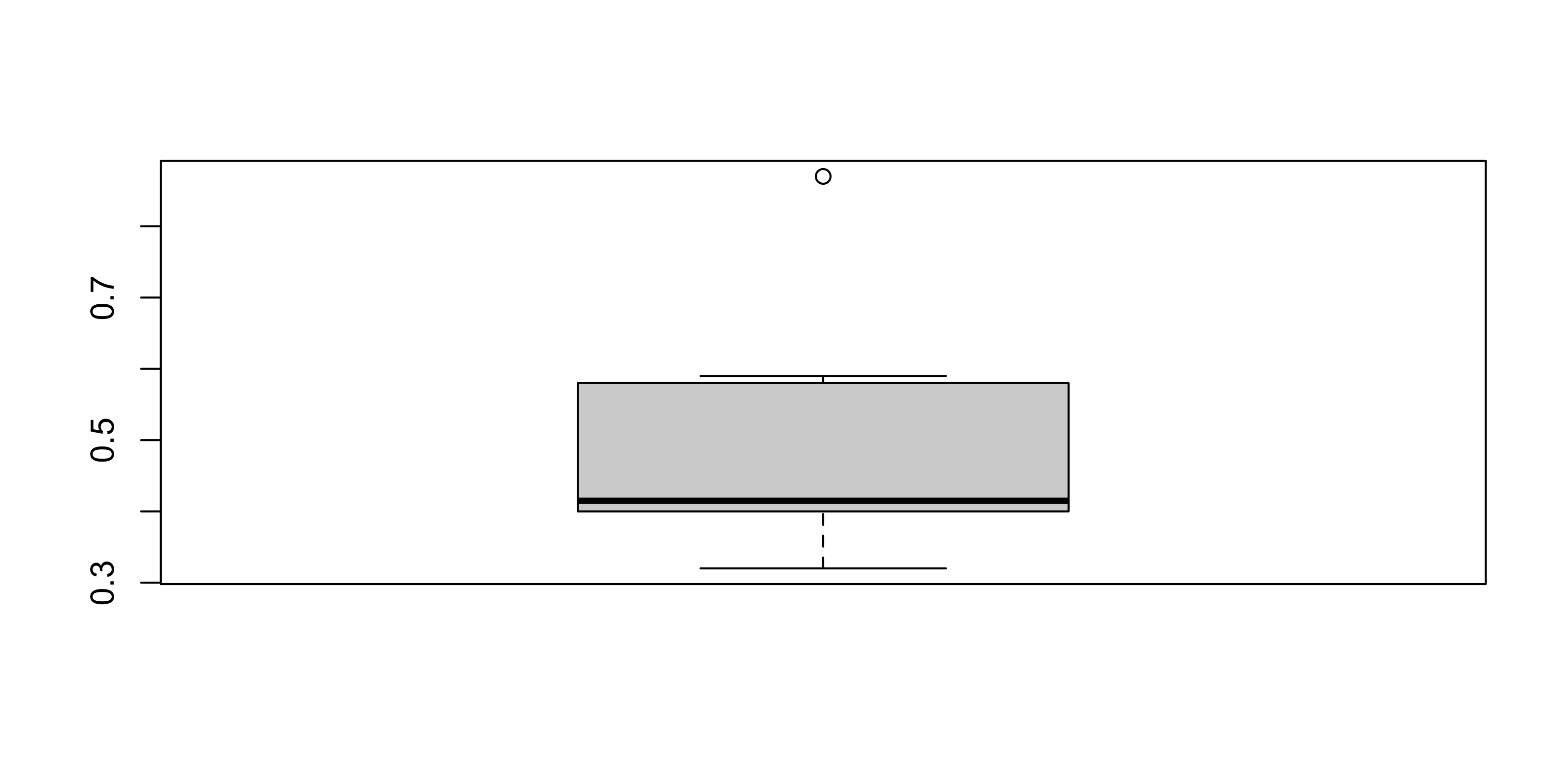
| Frazione di decessi | 0.38 | 0.32 | 0.59 | 0.58 | 0.41 | 0.87 | 0.54 | 0.4 | 0.42 | 0.4 |
Si individuino le distribuzioni di frequenze assolute cumulate, relative e relative cumulate della mortalità dei moscerini.
Si tracci il box-plot.
Si calcolino media e lo scarto quadratico medio.
Si calcoli un indice di variabilità robusto.
Schema della soluzione
La tabella delle frequenze è riportata qui di seguito.
| Frazione di decessi | 0.32 | 0.38 | 0.4 | 0.41 | 0.42 | 0.54 | 0.58 | 0.59 | 0.87 | |
|---|---|---|---|---|---|---|---|---|---|---|
| n_j | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| N_j | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| f_j | 0.1 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| F_j | 0.1 | 0.2 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
La media è pari a 0.491 mentre lo scarto quadratico medio è pari a 0.153. La mediana è pari a 0.415, mentre i quantili sono invece pari a
## 25% 75%
## 0.40 0.58È presente un outlier. Pertanto, il boxplot si ottiene come segue:
Un indice di variabilità robusto è il MAD, pari in questo caso a 0.065.