Statistica I

Esercizi 4: dati qualitativi, eterogeneità

Autore/Autrice
Affiliazione

Tommaso Rigon

Università degli Studi di Milano-Bicocca

Homepage

Alcune delle seguenti soluzioni sono state gentilmente fornite dal tutor di Statistica I dell’A.A. 2021/2022, Alex Alborghetti, che ringrazio. Le soluzioni sono state quindi riviste dal docente, che si assume le responsabilità di eventuali sviste ed errori.

Esercizio A (Tifosi e squadre di calcio)

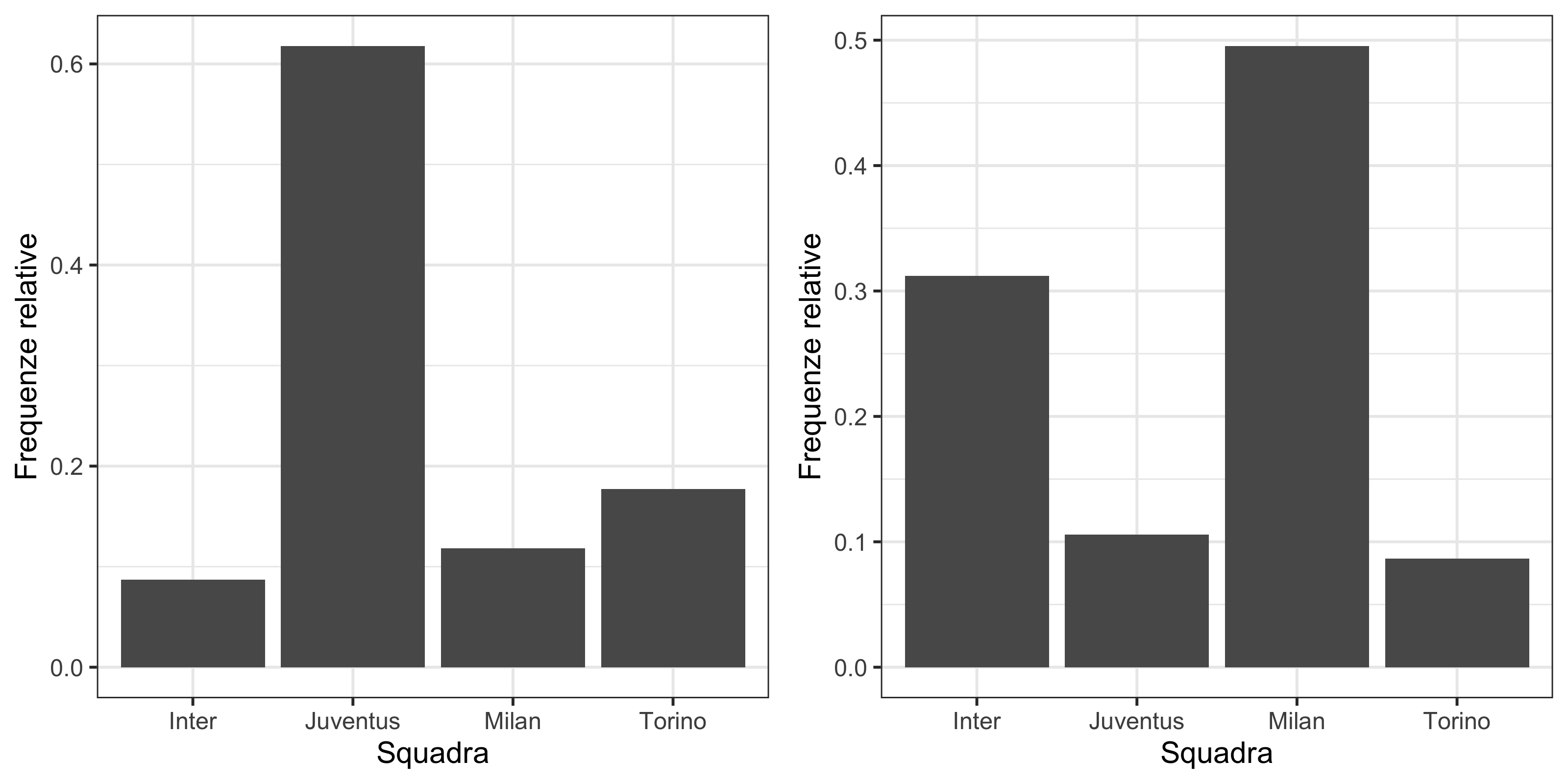
Da un sondaggio condotto da un giornale sportivo in due regioni sul tifo per le principali squadre di calcio si sono ottenuti i risultati che seguono:

Tifosi Inter Tifosi Milan Tifosi Torino Tifosi Juventus
Piemonte 331 450 675 2354
Lombardia 2125 3374 591 721

  1. Qual è la moda nelle due regioni?

  2. In quale delle due regioni c’è più omogeneità? Rispondere calcolando opportuni indici.

  3. Rappresentare graficamente i dati.

La moda, ovvero la modalità con frequenza più elevata, è “Juventus” per la regione Piemonte mentre è “Milan” per la regione Lombardia.

I calcoli necessari per valutare gli indici di Gini e di entropia sono riportati nelle tabelle che seguono.

Regione Piemonte

f_j f_j^2 \log{f_j} f_j \log{f_j}
Inter 0.0869 0.0075 -2.4433 -0.2123
Milan 0.1181 0.0140 -2.1361 -0.2523
Torino 0.1772 0.0314 -1.7307 -0.3066
Juventus 0.6178 0.3817 -0.4815 -0.2975
Totale 1 0.4346 -1.0687

Regione Lombardia

f_j f_j^2 \log{f_j} f_j \log{f_j}
Inter 0.3120 0.0973 -1.1648 -0.3634
Milan 0.4954 0.2454 -0.7024 -0.3480
Torino 0.0868 0.0075 -2.4445 -0.2121
Juventus 0.1059 0.0112 -2.2457 -0.2377
Totale 1 0.3615 -1.1612

Pertanto, l’indice di Gini per Piemonte e Lombardia sono pari a

G_\text{Piem} = 1 - 0.43 = 0.57, \qquad G_\text{Lomb} = 1 - 0.36 = 0.64. Gli indici normalizzati, in entrambi i casi, si ottengono moltiplicando i rispettivi indici per 4/3, ottenendo 0.76 per il Piemonte e 0.85 per la Lombardia. L’entropia per piemonte e Lombardia sono invece pari a:

H_\text{Piem} = 1.07, \qquad H_\text{Lomb} = 1.16.

I corrispettivi indici relativi si ottengono dividendo entrambi i termini per \log{4} \approx 1.39. Ne risulta 0.77 per il Piemonte e 0.84 per la Lombardia.

Quindi, entrambi gli indici normalizzati suggeriscono che il Piemonte è più omogeneo (meno variabile) in termini di tifoserie.

Una possibile rappresentazione grafica è costituita dai diagrammi a barre, che sono riportati nel seguito. Per facilitare il confronto tra le due regioni, sono state usate le frequenze relative.

Esercizio B (Customer satisfaction)

Siete il responsabile marketing di una grande azienda. Vi vengono forniti i dati di un’indagine di customer satisfaction svolta su 500 clienti di un’azienda concorrente, che voi mettete a confronto con un’indagine su 100 vostri clienti.

Sono disponibili le seguenti frequenze relative percentuali:

Per niente soddisfatti Poco soddisfatti Abbastanza soddisfatti Molto soddisfatti
Clienti azienda 14% 16% 48% 22%
Clienti concorrenza 10% 13% 62% 15%

  1. Rappresentare graficamente i dati usando le frequenze relative. Suggerimento: si veda l’Esercitazione 4.

  2. Analizzare le differenze riscontrate tra le due distribuzioni e sinteticamente indicare le caratteristiche delle due distribuzioni.

  3. Che cosa fareste al posto del responsabile di marketing dell’azienda in questione?

  4. Si calcoli la mediana della soddisfazione dei clienti nei due casi.

☠️ - Esercizio C

I clienti di un’azienza locale di vendita per corrispondenza sono stati classificati per provincia di residenza. Si conoscono le frequenze relative per le province di Trieste e Gorizia (si veda la tabella sottostante).

Provincia Frequenza relativa
Trieste 0.5
Gorizia 0.3
Udine ?
Pordenone ?

Sapendo che l’indice di Gini normalizzato è pari a G_\text{norm} = 0.85333, si dica quali sono le frequenze relative di Udine e Pordenone.

Il testo del problema indica che G_\text{norm} = \frac{4}{4-1} \left(1- \sum_{j=1}^kf_j^2\right) = 0.85333. Di conseguenza, si ottiene che \sum_{j=1}^kf_j^2 = -0.85333 \cdot \frac{4-1}{4} + 1, e pertanto: f_u^2 + f_p^2= -0.85333 \cdot \frac{4-1}{4} + 1 - 0.5^2 - 0.3^2 = 0.02.

Sappiamo inoltre che la somma delle frequenze relative è 1, ovvero:

0.5+0.3+f_p+f_u = 1.

Mettiamo a sistema queste due equazioni e risolviamo:

f_u^2 + f_p^2=0.02 \qquad (\text{i}), e f_u+f_p = 0.2 \qquad (\text{ii}).

Da (ii) si ricava f_u = 0.2-f_p. Sostituendo nella (i) 0.2^2 - 0.4 f_p + 2f_p^2 = 0.02,

cioè, risolvendo l’equazione di secondo grado: f_p = 0.1 (=f_u).

Esercizio D (Attività sportiva)

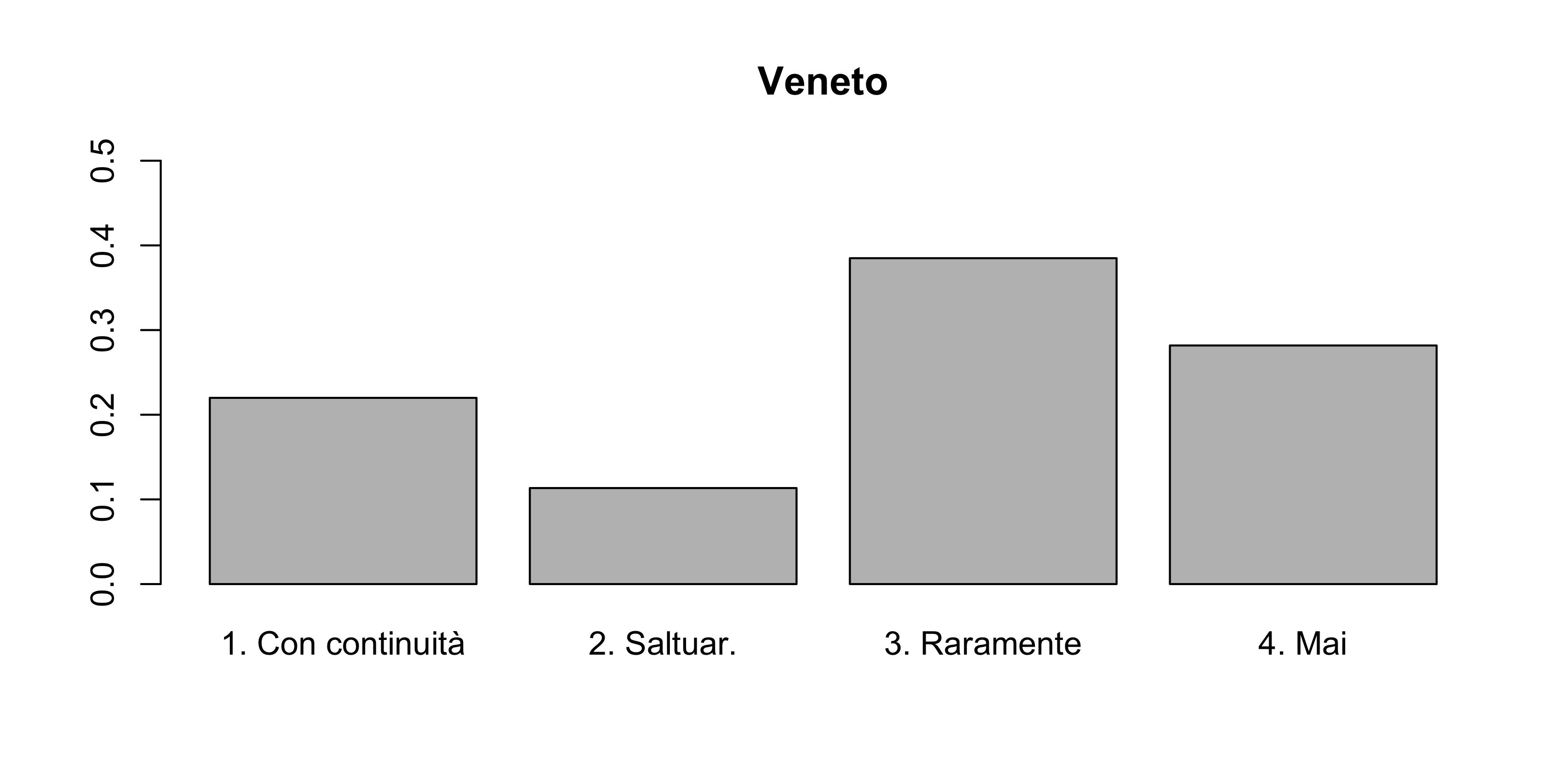
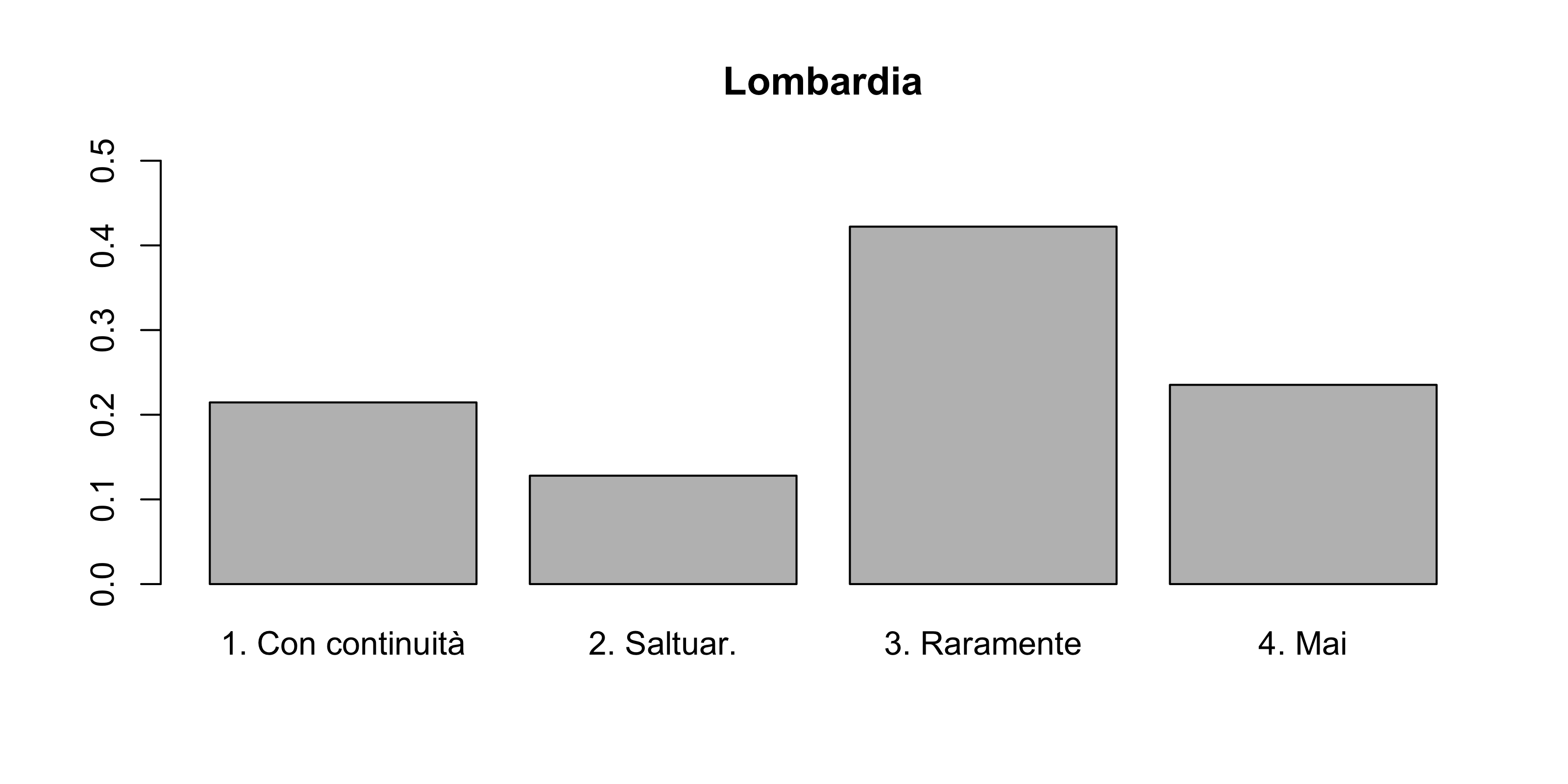
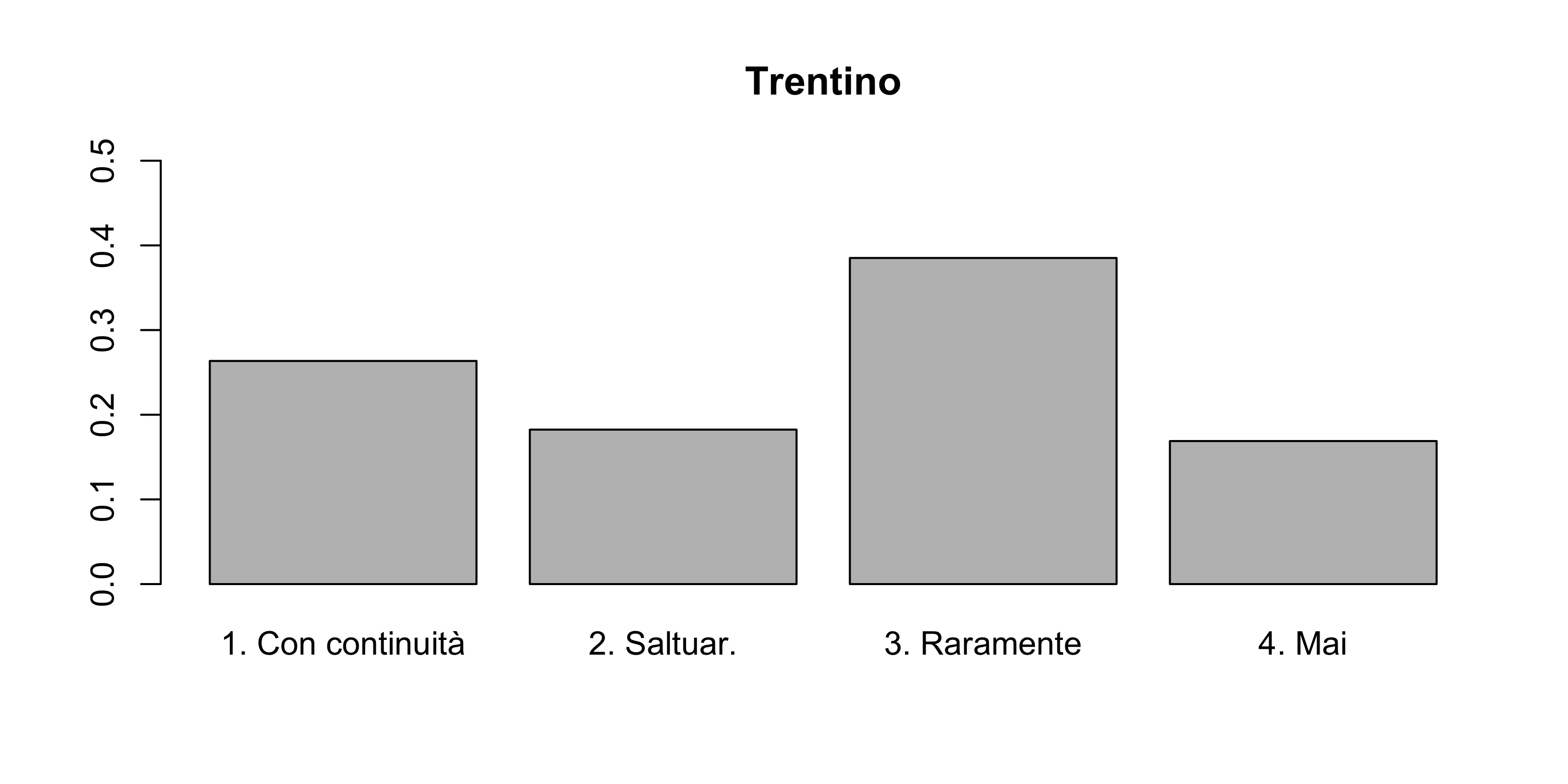
I risultati di un’indagine sulla pratica di una specifica attività sportiva tra le donne di tre regioni italiane sono riassunti nella tabella seguente.

Con continuità Saltuariamente Raramente Mai
Veneto 64 33 112 82
Lombardia 62 37 122 68
Trentino 78 54 114 50

  1. Qual è la moda della variabile “attività fisica” nella regione Lombardia?

  2. Si dia una rappresentazione grafica dei dati che permetta di confrontare le distribuzioni dell’attività fisica delle tre regioni.

  3. Si confronti l’eterogeneità della variabile “attività fisica” nelle tre regioni.

La moda della variabile “attività fisica” in Lombardia è “Raramente”.

Si noti che vanno utilizzate le frequenze relative, dato che la dimensione del campione è diversa nelle tre regioni. Possiamo confrontare l’eterogeneità tramite indice di Gini normalizzato. I risultati sono G_\text{norm, Lomb} = 0.939, G_\text{norm, Ven} = 0.948 e G_\text{norm, Trent} = 0.961. Per esercizio, provare a calcolare l’entropia di Shannon.

Esercizio E (Marmotte nelle alpi)

Una regione delle alpi è stata suddivisa in 6 zone di uguale dimensione e conformazione. Per ogni sottoarea è stato svolto un censimento delle marmotte presenti. I risultati ottenuti sono stati:

Zona A B C D E F
Frequenza assoluta 24 7 10 4 35 13

Si valuti se le marmotte sono equamente presenti nelle 6 zone con opportuni grafici ed indici.

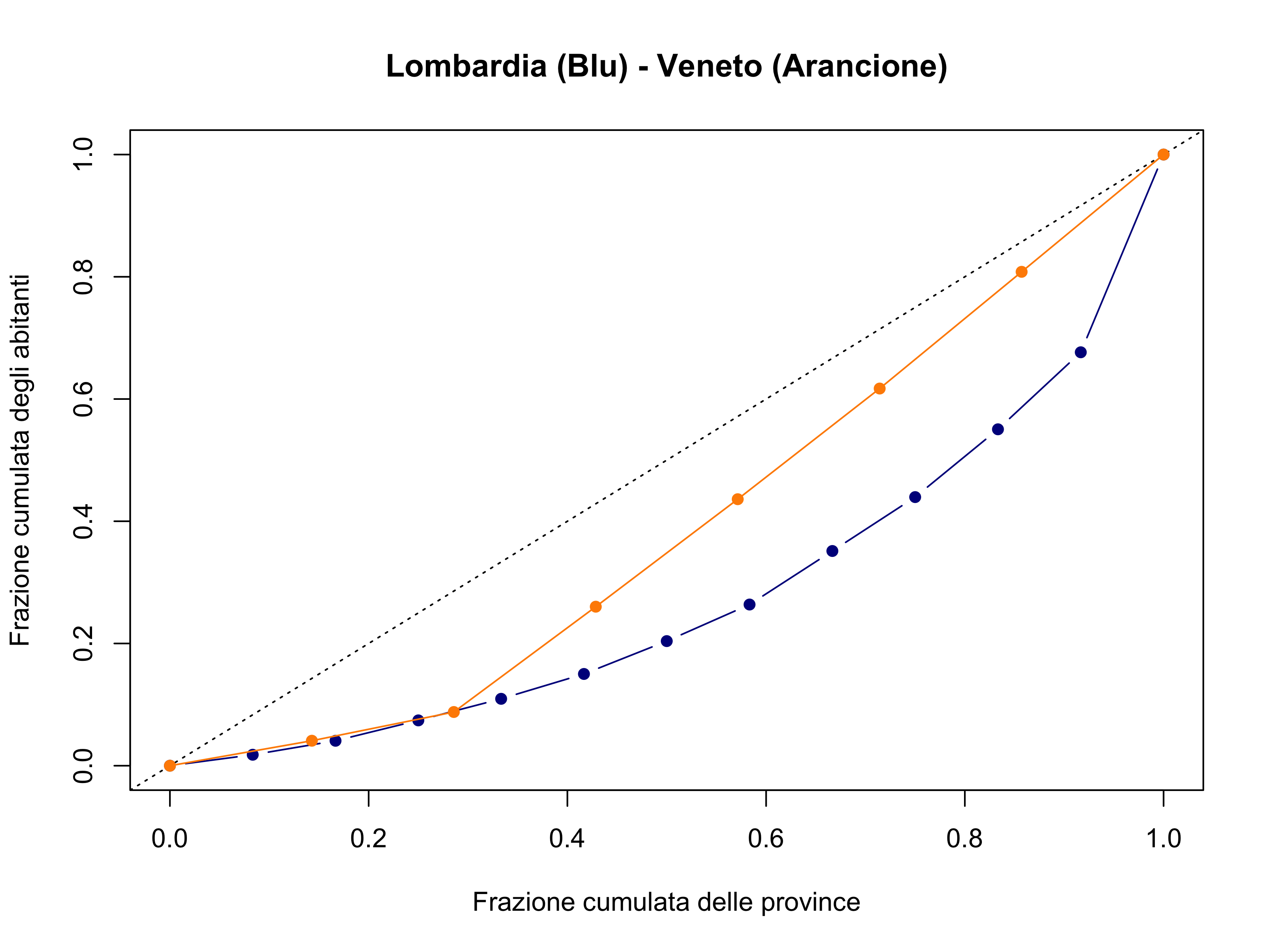
Esercizio F (Popolazione di Veneto e Lombardia)

Si consideri la popolazione residente delle province della regione Lombardia e Veneto, al primo Gennaio 2023. I dati ISTAT sono riportati nelle seguenti tabelle. Per quel che riguarda la regione Lombardia:

Provincia Popolazione residente Provincia Popolazione residente
Varese 877688 Pavia 534968
Como 595513 Cremona 351169
Sondrio 178472 Mantova 404696
Milano 3219391 Lecco 332043
Bergamo 1103768 Lodi 227495
Brescia 1253993 Monza e Brianza 871546

mentre per quel che riguarda il Veneto

Provincia Popolazione residente Provincia Popolazione residente
Belluno 197751 Treviso 876115
Rovigo 227418 Verona 923950
Venezia 833703 Padova 928374
Vicenza 850942 - -

  1. Si calcoli il rapporto di concentrazione di Gini per la regione Veneto e la regione Lombardia. Si commentino i risultati.

  2. Si disegnino quindi le curve di Lorenz corrispondenti.

Le tabelle seguenti costituiscono solamente uno schema della soluzione, non la soluzione stessa.

Provincia (Lombardia) Popolazione p_i q_i
Sondrio 178472 0.0833 0.0179
Lodi 227495 0.1667 0.0408
Lecco 332043 0.2500 0.0742
Cremona 351169 0.3333 0.1095
Mantova 404696 0.4167 0.1501
Pavia 534968 0.5000 0.2039
Como 595513 0.5833 0.2637
Monza e Brianza 871546 0.6667 0.3513
Varese 877688 0.7500 0.4395
Bergamo 1103768 0.8333 0.5504
Brescia 1253993 0.9167 0.6765
Milano 3219391 1.0000 1.0000

Di conseguenza, il rapporto di concentrazione di Gini per la regione Lombardia è \mathcal{R}_\text{lomb} = 1 - \frac{2}{n -1}\sum_{i=1}^{n-1} q_i = 1 - \frac{2}{11}(0.0179 + 0.0408 + 0.0742 + \cdots + 0.6765) = 0.4768. In alternativa, è possibile calcolare le differenza media semplice, ovvero \Delta_\text{lomb} = \frac{4}{n(n-1)}\left(\sum_{i=1}^n i x_{(i)}\right) - 2 \bar{x}_\text{lomb}\frac{n+1}{n-1} = \frac{4}{12 \cdot 11} \cdot 90772001 - 2 \cdot 829228.5 \frac{13}{11} = 790672.1.

dato che la media aritmetica è pari a \bar{x}_\text{lomb} = 829228.5. Pertanto,

\mathcal{R}_\text{lomb} = \frac{\Delta_\text{lomb}}{2 \bar{x}_\text{lomb}} = \frac{790672.1}{2 \cdot 829228.5}= 0.4768. Per quel che riguarda la regione Veneto, con conti analoghi si ottiene anzitutto la tabella seguente:

Provincia (Veneto) Popolazione p_i q_i
Belluno 197751 0.1429 0.0409
Rovigo 227418 0.2857 0.0879
Venezia 833703 0.4286 0.2602
Vicenza 850942 0.5714 0.4361
Treviso 876115 0.7143 0.6172
Verona 923950 0.8571 0.8081
Padova 928374 1.0000 1.0000

tramite la quale si perviene al rapporto di concentrazione di Gini pari a \mathcal{R}_\text{ven} = 0.2499. Le curve di Lorenz corrispondenti sono disegnate nel seguito.