Statistica I
Esercizi 5: covarianza, correlazione, regressione lineare semplice
Homepage
Esercizio A (Tabacco e bevande alcoliche)
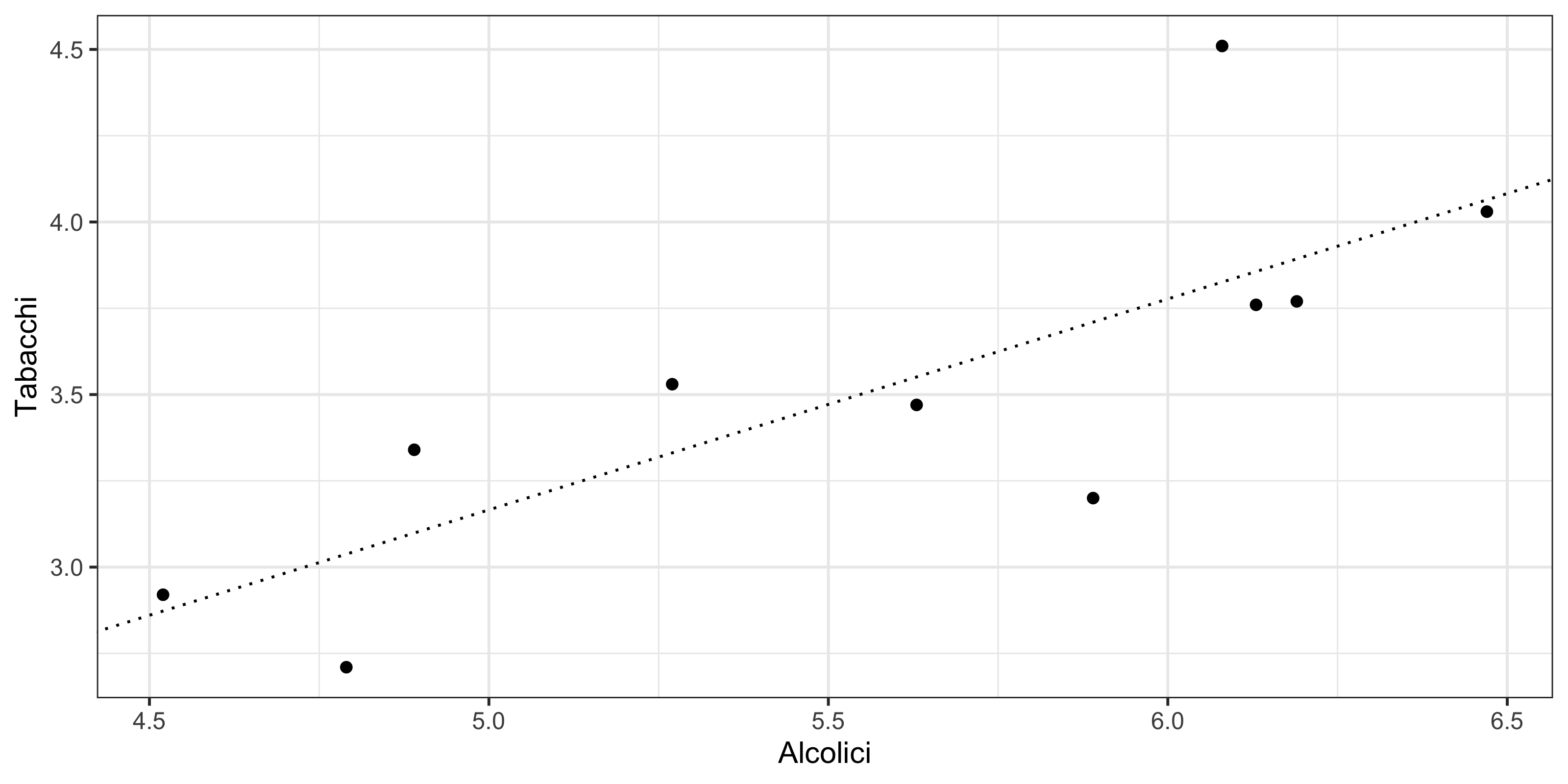
I risultati di un’indagine del governo britannico sulla spesa delle famiglie possono essere utilizzati per investigare sulla relazione tra l’ammontare speso per i tabacchi e quello speso per le bevande alcoliche.
La seguente tabella riporta, per n = 10 regioni della Gran Bretagna, la spesa settimanale media per famiglia per i due capitoli di spesa, espressa in sterline. I dati sono riferiti al 1981.
| Regione | Alcolici | Tabacchi |
|---|---|---|
| North | 6.47 | 4.03 |
| Yorkshire | 6.13 | 3.76 |
| Northeast | 6.19 | 3.77 |
| East Midlands | 4.89 | 3.34 |
| West Midlands | 5.63 | 3.47 |
| East Anglia | 4.52 | 2.92 |
| Southeast | 5.89 | 3.2 |
| Southwest | 4.79 | 2.71 |
| Wales | 5.27 | 3.53 |
| Scotland | 6.08 | 4.51 |
Si valuti la funzione di regressione tra le due variabili (usando la variabile alcolici come esplicativa), ripercorrendo gli stessi punti svolti nell’esercitazione 5. In particolare:
- Si disegnino i dati tramite un diagramma a dispersione.
- Si ottengano medie e varianze di x ed y.
- Si ottengano le stime ai minimi quadrati.
- Si disegni la retta di regressione stimata nel diagramma a dispersione.
- Si ottengano i valori previsti ed i residui della regressione.
- Si ottenga la varianza residuale.
- Si calcoli R^2 e correlazione \rho.
Schema della soluzione
In primo luogo disegniamo graficamente i dati tramite un diagramma a dispersione
Valutiamo quindi le principali quantità d’interesse, dove x_1,\dots,x_{10} rappresentano gli alcolici e y_1,\dots,y_{10} rappresentano invece i tabacchi. Di conseguenza, avremo che:
\sum_{i=1}^nx_i y_i = 199.38, \qquad \sum_{i=1}^nx_i = 55.86, \qquad \sum_{i=1}^ny_i = 35.24.
È inoltre possibile calcolare le seguenti quantità
\sum_{i=1}^nx_i^2 = 316.169, \qquad \sum_{i=1}^ny_i^2 = 126.7. Utilizzando le quantità del punto precedente, possiamo quindi ottenere la stima ai minimi quadrati (\hat{\alpha},\hat{\beta}) di un modello di regressione lineare semplice. In particolare, avremo che:
\hat{\beta} = \frac{\text{cov}(x,y)}{\text{var}(x)} = \frac{19.938 - 5.586\times 3.524}{31.617 - 5.586^2}= 0.611. Si ha infatti che \text{cov}(x,y) = 19.938 - 5.586\times 3.524 = 0.252936 mentre \text{var}(x) = 31.617 - 5.586^2 = 0.4136. Inoltre avremo che:
\hat{\alpha} = \bar{y} - \hat{\beta} \bar{x} = \frac{35.24}{10} - 0.611\frac{55.86}{10} = 0.111. I valori previsti si ottengono quindi tramite l’equazione:
\hat{y}_i = 0.111 + 0.611x_i.
Per comodità, riportiamo i valori previsti ed i residui nella seguente tabella
| x_i | y_i | \hat{y}_i | r_i |
|---|---|---|---|
| 6.47 | 4.03 | 4.06 | -0.03 |
| 6.13 | 3.76 | 3.86 | -0.10 |
| 6.19 | 3.77 | 3.89 | -0.12 |
| 4.89 | 3.34 | 3.10 | 0.24 |
| 5.63 | 3.47 | 3.55 | -0.08 |
| 4.52 | 2.92 | 2.87 | 0.05 |
| 5.89 | 3.20 | 3.71 | -0.51 |
| 4.79 | 2.71 | 3.04 | -0.33 |
| 5.27 | 3.53 | 3.33 | 0.20 |
| 6.08 | 4.51 | 3.83 | 0.68 |
Per valutare la bontà d’adattamento del modello usando l’indice R^2 si può procedere in due modi: i) calcolare il coefficiente di correlazione \rho ed elevarlo al quadrato, oppure ii) attraverso il calcolo della varianza dei residui.
Dalla precedente tabella, so ottiene che \text{var}(r) = n^{-1}\sum_{i=1}^n r_i^2 = 0.096. Pertanto, otteniamo che
R^2 = 1 - \frac{\text{var}(r)}{\text{var}(y)} = 1 - \frac{0.096}{12.67 - 3.524^2} = 0.62. Alternativamente avremmo potuto calcolare l’indice di correlazione \rho = \frac{\text{cov}(x,y)}{\sqrt{\text{var}(x)}\sqrt{\text{var}(y)}} = \frac{0.2529}{\sqrt{0.4136 \times 0.2514}} = 0.78428. E pertanto si otterà che R^2 = \rho^2 = 0.62. Concludiamo l’analisi rappresentano la retta di regressione sovrapposta ai dati.
Esercizio B (Regressione con variabili standardizzate)
Si considerino due variabili statistiche x ed y e siano \hat{\alpha} e \hat{\beta} le stime ai minimi quadrati dei parametri del modello di regressione y = \alpha + \beta x.
Si considerino quindi le variabili z_i = \frac{x_i − \bar{x}}{\sigma_x}, \qquad w_i = \frac{y_i - \bar{y}}{\sigma_y},\qquad i=1,\dots,n. Inoltre, si consideri il modello di regressione w = \gamma + \delta z.
Si ottengano i coefficienti ai minimi quadrati \hat{\gamma} e \hat{\delta}.
Cosa si può dire circa le devianze residui dei due modelli? E degli indici R^2?
Esercizio C (I dati di Anscombe)
Sono date le seguenti osservazioni da 4 regressori e 4 variabili dipendenti
| x^{(1)} | x^{(2)} | x^{(3)} | x^{(4)} | y^{(1)} | y^{(2)} | y^{(3)} | y^{(4)} |
|---|---|---|---|---|---|---|---|
| 10 | 10 | 10 | 8 | 8.04 | 9.14 | 7.46 | 6.58 |
| 8 | 8 | 8 | 8 | 6.95 | 8.14 | 6.77 | 5.76 |
| 13 | 13 | 13 | 8 | 7.58 | 8.74 | 12.74 | 7.71 |
| 9 | 9 | 9 | 8 | 8.81 | 8.77 | 7.11 | 8.84 |
| 11 | 11 | 11 | 8 | 8.33 | 9.26 | 7.81 | 8.47 |
| 14 | 14 | 14 | 8 | 9.96 | 8.10 | 8.84 | 7.04 |
| 6 | 6 | 6 | 8 | 7.24 | 6.13 | 6.08 | 5.25 |
| 4 | 4 | 4 | 19 | 4.26 | 3.10 | 5.39 | 12.50 |
| 12 | 12 | 12 | 8 | 10.84 | 9.13 | 8.15 | 5.56 |
| 7 | 7 | 7 | 8 | 4.82 | 7.26 | 6.42 | 7.91 |
| 5 | 5 | 5 | 8 | 5.68 | 4.74 | 5.73 | 6.89 |
Si calcoli il coefficiente di correlazione per ciascuna delle coppie di variabili x^{(j)} e y^{(j)}, per j=1,\dots,4.
Si disegni il grafico a dispersione per ciascuna coppia di variabili considerata al punto precedente. Si commentino i risultati ottenuti in relazione al punto precedente.
☠️ - Esercizio D
Per n = 10 paesi dell’Unione Europea si è osservato il prezzo in euro di un litro di benzina (variabile x) ed il numero di veicoli pro-capite circolanti (variabile y). I dati si riferiscono alla fine degli anni '90. Si conoscono i seguenti risultati: \sum_{i=1}^nx_i = 8.79, \qquad \sum_{i=1}^ny_i = 8.63, \qquad \frac{1}{n}\sum_{i=1}^nx_i^2 = 0.77385, \qquad \frac{1}{n}\sum_{i=1}^ny_i^2 = 0.7695. Inoltre, è noto che la somma dei residui al quadrato del modello di regressione y = \alpha + \beta x sono pari a
\sum_{i=1}^nr_i^2 = 0.01157.
Sulla base di queste informazioni, si ottengano le stime ai minimi quadrati \hat{\alpha} e \hat{\beta} e si ottenga un indice di bontà di adattamento. Si assuma inoltre che le variabili x ed y siano negativamente correlate.
Suggerimento. Si cominci ottenendo il valore R^2 e si ragioni quindi sulla definizione di \hat{\beta}.
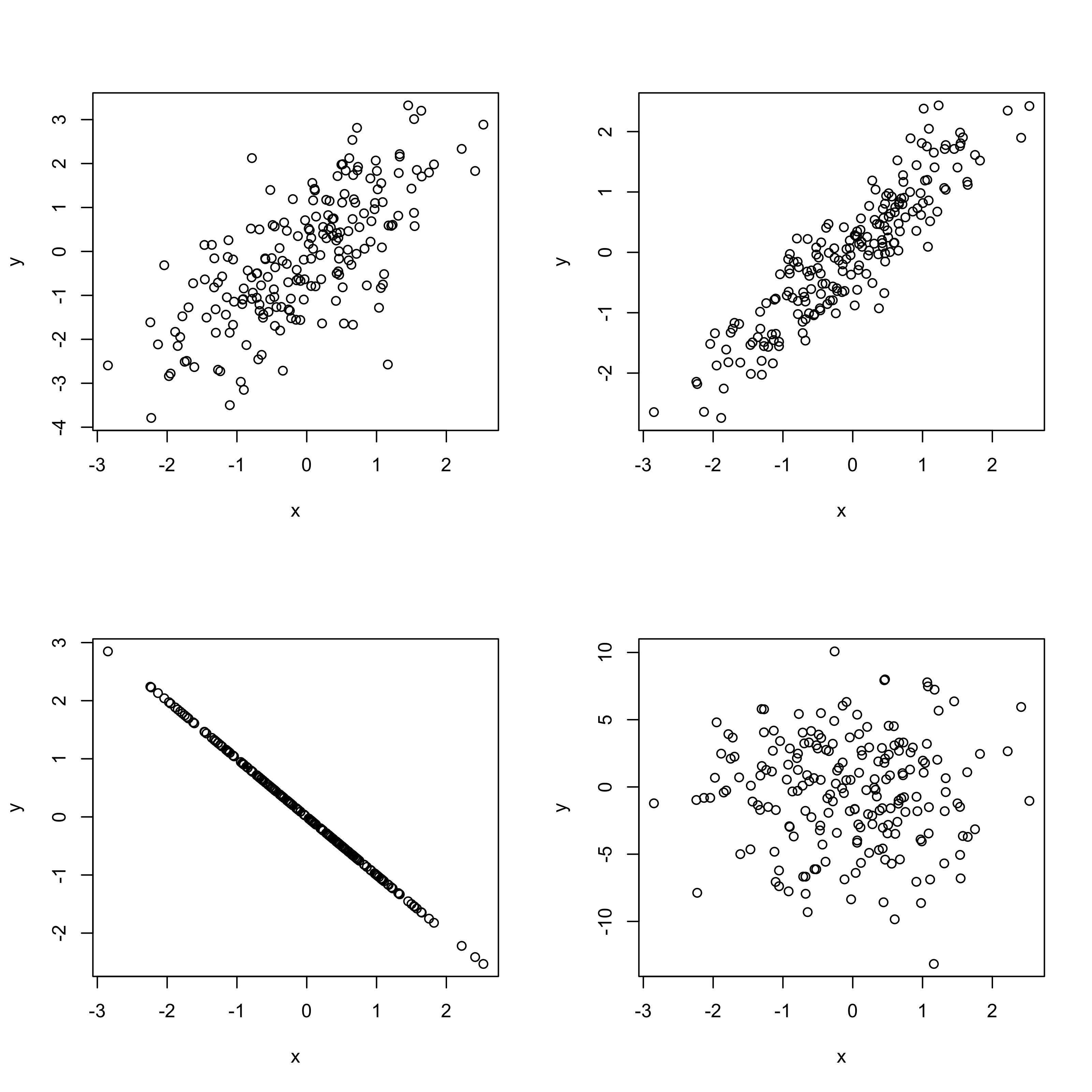
Esercizio E
Nella figura che segue sono riportati i diagrammi a dispersione di 4 coppie di variabili. Ad esse corrispondono i coefficienti di correlazione \rho pari a -1,0,0.7,0.9. Si dica a quale grafico corrisponde ciascun coefficiente.
