Statistica I

Esercizi 7: tabelle di contingenza

Autore/Autrice
Affiliazione

Tommaso Rigon

Università degli Studi di Milano-Bicocca

Homepage

Alcune delle seguenti soluzioni sono state gentilmente fornite dal tutor di Statistica I dell’A.A. 2021/2022, Alex Alborghetti, che ringrazio. Le soluzioni sono state quindi riviste dal docente, che si assume le responsabilità di eventuali sviste ed errori.

Esercizio A

La seguente tabella di contingenza mostra come n = 319 studenti universitari di varie università si distribuiscono sulla base delle due variabili “Tipo di maturità” e “Numero di esami superati durante il primo anno”.

0 - 1 2 - 5 5 +
Maturità classica 10 67 31
Maturità scientifica 4 52 36
Altre 14 65 40

Analizzare la dipendenza (in distribuzione) esistente tra le due variabili con gli strumenti a voi noti.

Per misurare la dipendenza in distribuzione di x da y utilizziamo l’indice \chi^2 normalizzato, che si basa sulla distanza tra frequenze attese e frequenze osservate, così definito:

\chi^2_\text{norm} = \frac{1}{n\min(h-1, k-1)} \sum_{i=1}^h\sum_{j=1}^k \frac{(n_{ij} - \hat{n}_{ij})^2}{\hat{n}_{ij}}.

Posto h = k = 3, calcoliamo le frequenze attese \hat{n}_{ij} = (n_{i+}n_{+j})/n. Partendo dalla seguente:

0-1 2-5 5+
Maturità classica 10 67 31 108
Maturità scientifica 4 52 36 92
Altre 14 65 40 119
28 184 107 n = 319

Applicando la formula:

0-1 2-5 5+
Maturità classica 9.48 62.3 36.23 108
Maturità scientifica 8.08 53.07 30.86 92
Altre 10.45 68.64 39.92 119
28 184 107 n = 319

Allora:

\chi^2_\text{norm} \approx 0.01.

Possiamo quindi concludere che, praticamente, esiste indipendenza in distribuzione tra le due variabili, ovvero, sulla base dei dati disponibili, il titolo di studio ottenuto alle superiori non sembra essere connesso con il numero di esami dati al primo anno di università, o comunque in modo molto lieve.

Esercizio B

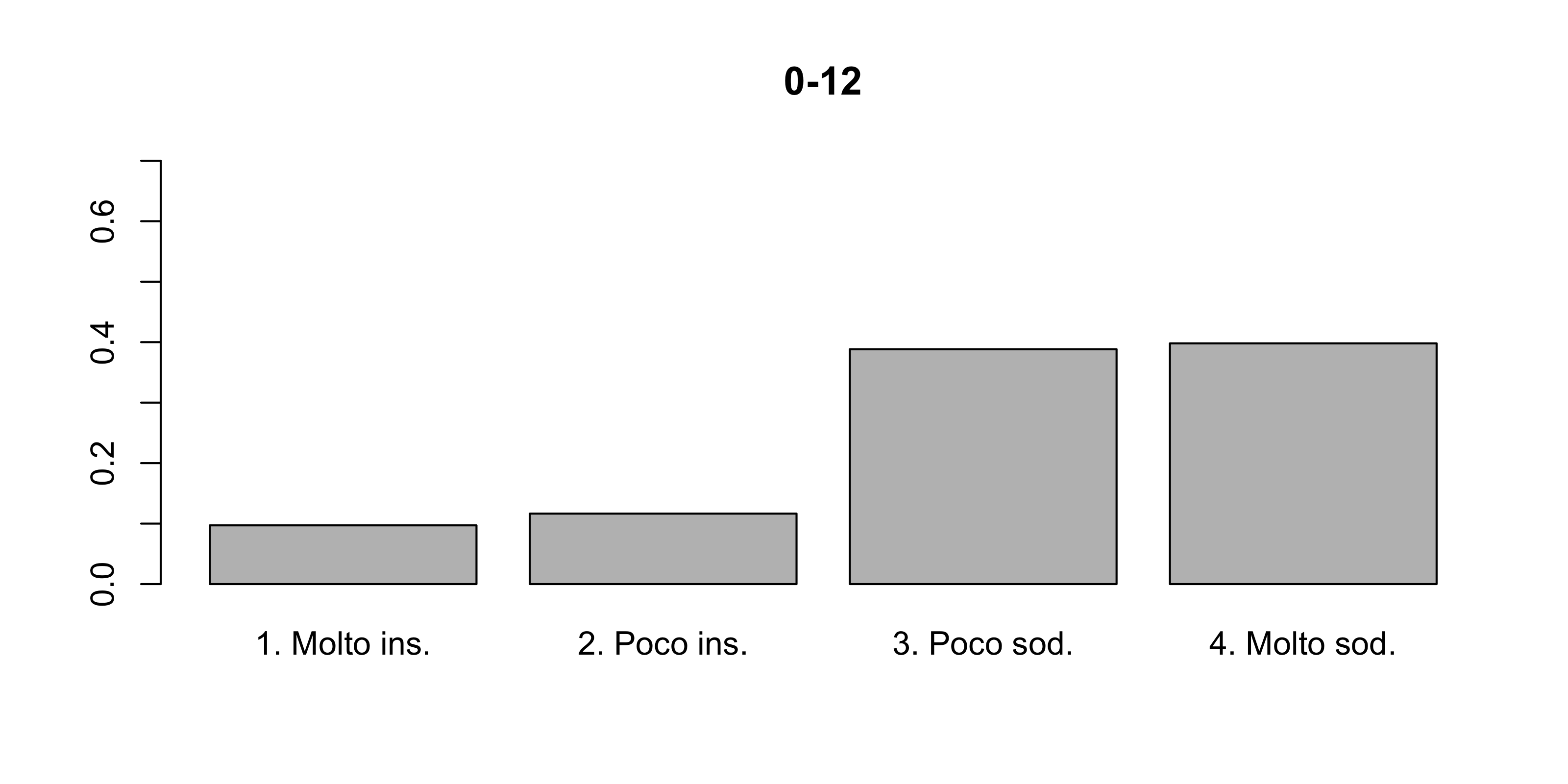
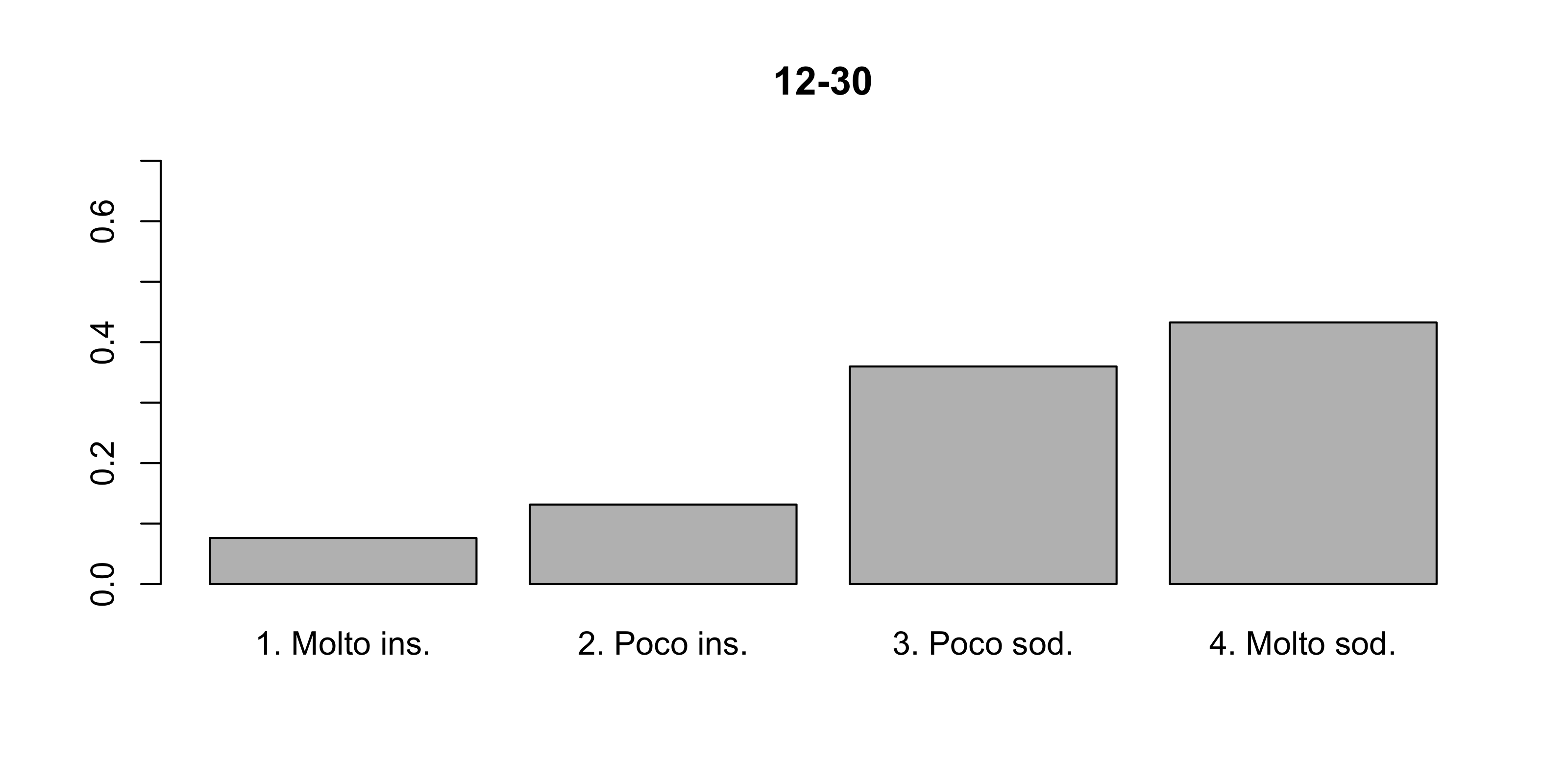
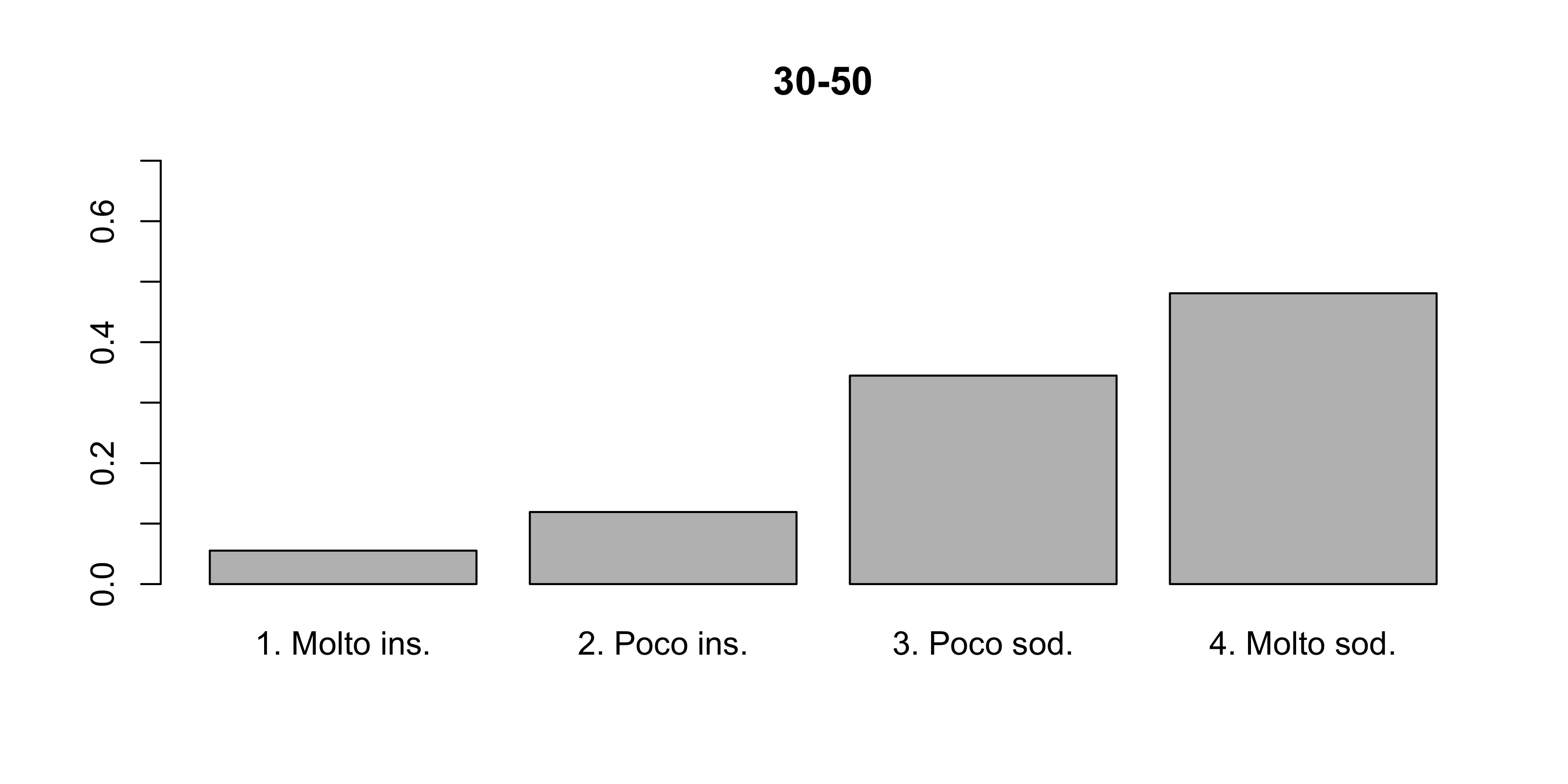
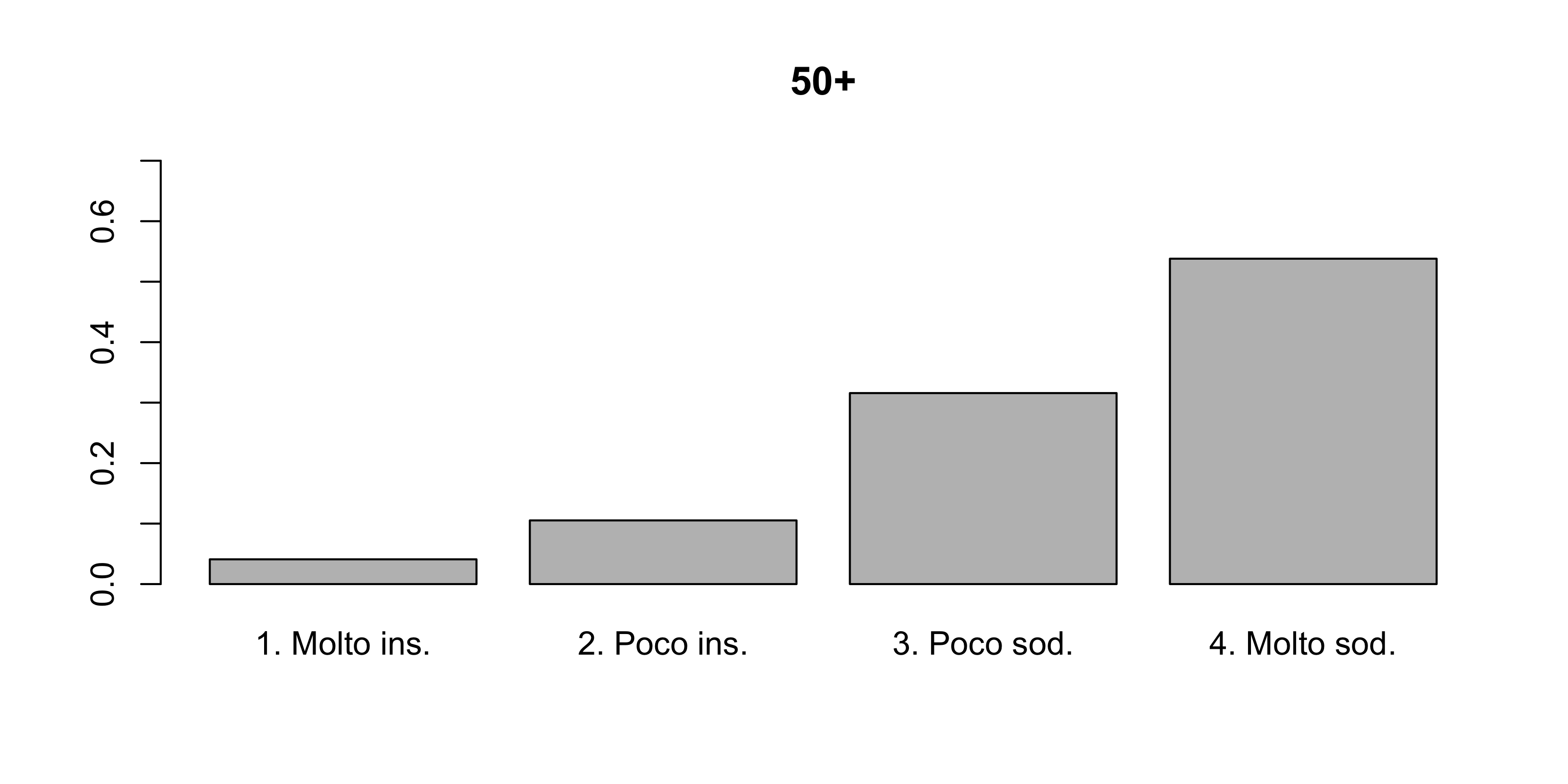
Un’azienda vuole conoscere se la soddisfazione nel lavoro può essere determinata anche dallo stipendio del dipendente. A questo scopo ha intervistato tutti i suoi dipendenti e li ha classificati in base al reddito, come riportato nella tabella seguente.

Molto insoddisfatto Poco insoddisfatto Poco soddisfatto Molto soddisfatto
0 - 12 20 24 80 82
12 - 30 22 38 104 125
30 - 50 13 28 81 113
50+ 7 18 54 92

  1. Attraverso un opportuno indice statistico si dica se esiste una dipendenza in distribuzione tra le due variabili.

  2. Si illustri le distribuzioni condizionate della variabile soddisfazione dato il reddito.

  3. Al crescere dello stipendio aumenta la soddisfazione?

Riportiamo la tabella calcolando le frequenze marginali:

Molto ins. Poco ins. Poco sodd. Molto sodd.
0-12 20 24 80 82 206
12-30 22 38 104 125 289
30-50 13 28 81 113 235
50+ 7 18 54 92 171
62 108 319 412 n = 901

Come in precedenza, analizziamo la dipendenza in distribuzione tramite l’indice \chi^2, costruiamo pertanto la tabella delle frequenze attese:

Molto ins. Poco ins. Poco sodd. Molto sodd.
0-12 14.2 24.7 72.9 94.2 206
12-30 19.9 34.6 102.3 132.2 289
30-50 16.2 28.2 83.2 107.5 235
50+ 11.8 20.5 60.5 78.2 171
62 108 319 412 n = 901

Possiamo quindi concludere che, praticamente, esiste indipendenza in distribuzione tra le due variabili. Qui sotto ne viene fornita la rappresentazione grafica.

Esercizio C

Nella tabella seguente è riportato il tipo di allattamento e la presenza o meno di difetti nella dentatura del neonato.

Denti normali Malocclusione
Allattamento naturale 4 16
Allattamento artificiale 1 21

  1. Si dica attraverso un opportuno indice statistico appropriato se vi è associazione tra le due variabili rilevate.

  2. Si può inoltre affermare che il tipo di allattamento provoca difetti nella dentatura dei neonati?

Riportiamo la tabella calcolando le frequenze marginali:

Denti normali Malocclusione
Allattamento naturale 4 16 20
Allattamento artificiale 1 21 22
5 37 n= 42

Calcoliamo la tabella delle frequenze attese:

Denti normali Malocclusione
Allattamento naturale 2.4 17.6 20
Allattamento artificiale 2.6 19.4 22
5 37 n= 42

Allora:

\chi^2_\text{norm} \approx 0.06.

Esiste quindi una lieve connessione tra il tipo di allattamento e i difetti nella dentatura del neonato. Non si può, però, affermare con certezza che passando da un tipo di allattamento ad un altro siano più frequenti difetti nella dentatura neonatale, dal momento che aver trovato una connessione non significa necessariamente aver trovato un rapporto di causalità. Inoltre, la numerosità campionaria è piuttosto ridotta.

☠️ - Esercizio D

Nella tabella che segue sono riportare le frequenze congiunte percentuali del numero di telefoni cellulari presenti in Italia a seconda delle diverse aree geografiche e di due fornitori. Si sa inoltre che il numero di clienti TIM è il 50\% più alto di quelli di Vodafone e che i clienti di TIM sono 9 milioni.

Nord Centro Sud
TIM 25.2 ? 16.8
Vodafone ? 12 9.2

  1. Completare la tabella.

  2. Al di là dei valori assoluti, quale delle due compagnie ha maggiore capacità di penetrazione commerciale al nord?

  3. C’è associazione tra le due variabili?