R per l’analisi statistica multivariata

Unità G: analisi descrittiva dei dati titanic

Autore/Autrice
Affiliazione

Tommaso Rigon

Università degli Studi di Milano-Bicocca

Argomenti affrontati

  • Dati qualitativi
  • Tabelle di contingenza
  • Distribuzioni condizionate
  • Indipendenza e indice di connessione \chi^2
Nota

Gli esercizi R associati sono disponibili a questo link

Descrizione del problema

Dopo il disastro del Titanic, una commissione d’inchiesta del British Board of Trade ha compilato una lista di tutti i 1316 passeggeri includendo le seguenti informazioni:

  • l’esito (salvato, non salvato)
  • la classe (I, II, III) in cui viaggiavano
  • il sesso, l’età, etc.

In questa unità ci limitiamo a considerare le informazioni sull’esito e la classe.

Nota

Ovviamente, si tratta degli stessi dati considerati nell’unità O del corso Statistica I.

Importazione dei dati titanic

Come fatto in precedenza, anzitutto è necessario scaricare il file titanic.csv e salvarlo nel proprio computer. Link al file

titanic <- read.table("../dataset/titanic.csv", header = TRUE, sep = ",", stringsAsFactors = TRUE)

In alternativa, possiamo semplice ottenerli usando il link:

path <- "https://tommasorigon.github.io/introR/dataset/titanic.csv"
titanic <- read.table(path, header = TRUE, sep = ",", stringsAsFactors = TRUE)
str(titanic)
'data.frame':   1316 obs. of  2 variables:
 $ Salvato: Factor w/ 2 levels "No","Si": 2 2 2 2 2 2 2 2 2 2 ...
 $ Classe : Factor w/ 3 levels "I","II","III": 1 1 1 1 1 1 1 1 1 1 ...

Le frequenze assolute e relative (marginali)

Possiamo ottenere le frequenze assolute (marginali) delle due variabili usando il comando summary:

summary(titanic)
 Salvato  Classe   
 No:817   I  :325  
 Si:499   II :285  
          III:706

Ovviamente, possiamo ottenere le frequenze assolute e relative anche usando il comando table. Ad esempio per la variabile classe, possiamo utilizzare:

freq_abs_classe <- table(titanic$Classe)
freq_rel_classe <- freq_abs_classe / sum(freq_abs_classe)
tab_summary <- cbind(freq_abs_classe, freq_rel_classe)
tab_summary
    freq_abs_classe freq_rel_classe
I               325       0.2469605
II              285       0.2165653
III             706       0.5364742

Frequenze congiunte

Una sintesi che possiamo operare consiste nel costruire una tabella, detta tabella di contingenza oppure tabella a doppia entrata.

In R si usa anche in questo caso il comando table, con due argomenti:

tab <- table(titanic$Salvato, titanic$Classe)
tab
    
       I  II III
  No 122 167 528
  Si 203 118 178

In questa tabella sono riportate le frequenze congiunte, ad esempio, il valore 203 rappresenta il numero di passeggeri che viaggiavano in I classe e che sono sopravvissuti.

Tabella di contingenza

Siano x ed y due variabili aventi modalità c_1,\dots,c_h e d_1,\dots,d_k, rispettivamente.

Una tabella di contingenza (a due variabili) per le coppie di dati (x_1,y_1),\dots,(x_n,y_n) si presenta nella seguente forma:

Variabile y
Variabile x d_1 \dots d_j \dots d_k Totale
c_1 n_{11} \dots n_{1j} \dots n_{1k} n_{1+}
\vdots \vdots \vdots \vdots \vdots
c_i n_{i1} \dots n_{ij} \dots n_{ik} n_{i+}
\vdots \vdots \vdots \vdots \vdots
c_h n_{h1} \dots n_{hj} \dots n_{hk} n_{h+}
Totale n_{+1} \dots n_{+j} \dots n_{+k} n

La frequenza n_{ij} è il numero di unità statistica che presentano contemporaneamente le modalità c_i e d_j.

Tabella di contingenza, frequenze relative

Dividendo per n ciascun termine della precedente tabella, si ottiene inoltre:

Variabile y
Variabile x d_1 \dots d_j \dots d_k Totale
c_1 f_{11} \dots f_{1j} \dots f_{1k} f_{1+}
\vdots \vdots \vdots \vdots \vdots
c_i f_{i1} \dots f_{ij} \dots f_{ik} f_{i+}
\vdots \vdots \vdots \vdots \vdots
c_h f_{h1} \dots f_{hj} \dots f_{hk} f_{h+}
Totale f_{+1} \dots f_{+j} \dots f_{+k} 1

La frequenza relativa f_{ij} = n_{ij} / n è quindi la frazione di osservazioni che presentano contemporaneamente le modalità c_i e d_j.

Frequenze congiunte & marginali

Le tabelle descritte nei paragrafi precedenti si ottengono in R come segue:

addmargins(tab) # Aggiunge le distribuzioni marginali (assolute)
     
         I   II  III  Sum
  No   122  167  528  817
  Si   203  118  178  499
  Sum  325  285  706 1316
tab_rel <- prop.table(tab) # Comando alternativo: table(tab) / sum(tab)
tab_rel
    
              I         II        III
  No 0.09270517 0.12689970 0.40121581
  Si 0.15425532 0.08966565 0.13525836
addmargins(tab_rel) # Aggiunge le distribuzioni marginali relative
     
               I         II        III        Sum
  No  0.09270517 0.12689970 0.40121581 0.62082067
  Si  0.15425532 0.08966565 0.13525836 0.37917933
  Sum 0.24696049 0.21656535 0.53647416 1.00000000

Distribuzioni condizionate I

Distribuzione condizionata (x \mid y = d_j)

La j-esima colonna mostra la distribuzione di x condizionata ad y = d_j oppure, equivalentemente, la distribuzione di x dato y = d_j.

Distribuzione x \mid y = d_j c_1 \dots c_i \dots c_h Totale
Frequenze assolute n_{1j} \dots n_{ij} \dots n_{hj} n_{+j}
Frequenze relative n_{1j} / n_{+j} \dots n_{ij} / n_{+j} \dots n_{hj} / n_{+j} 1

Distribuzione condizionata (y \mid x = c_i)

La i-esima riga mostra la distribuzione di y condizionata ad x = c_i oppure, equivalentemente, la distribuzione di y dato x = c_i.

Distribuzione y \mid x = c_i d_1 \dots d_j \dots d_k Totale
Frequenze assolute n_{i1} \dots n_{ij} \dots n_{ik} n_{i+}
Frequenze relative n_{i1} / n_{i+} \dots n_{ij} / n_{i+} \dots n_{ik} / n_{i+} 1

Distribuzioni condizionate II

Il comando prop.table consente anche di calcolare le frequenze condizionate relative.

La distribuzione di ciascuna classe, condizionata all’esito è:

prop.table(tab, 1)
    
             I        II       III
  No 0.1493268 0.2044064 0.6462668
  Si 0.4068136 0.2364729 0.3567134

La distribuzione di ciascun esito, condizionata alla classe è:

prop.table(tab, 2)
    
             I        II       III
  No 0.3753846 0.5859649 0.7478754
  Si 0.6246154 0.4140351 0.2521246

Rappresentazioni grafiche

È possibile rappresentare graficamente i dati di una tabella di contingenza tramite un diagramma a barre, che in R è implementato tramite il comando barplot.

Una rappresentazione grafica delle frequenze congiunte è pertanto la seguente:

barplot(tab, beside = TRUE, legend.text = TRUE) # Beside = TRUE "affianca" i rettangoli.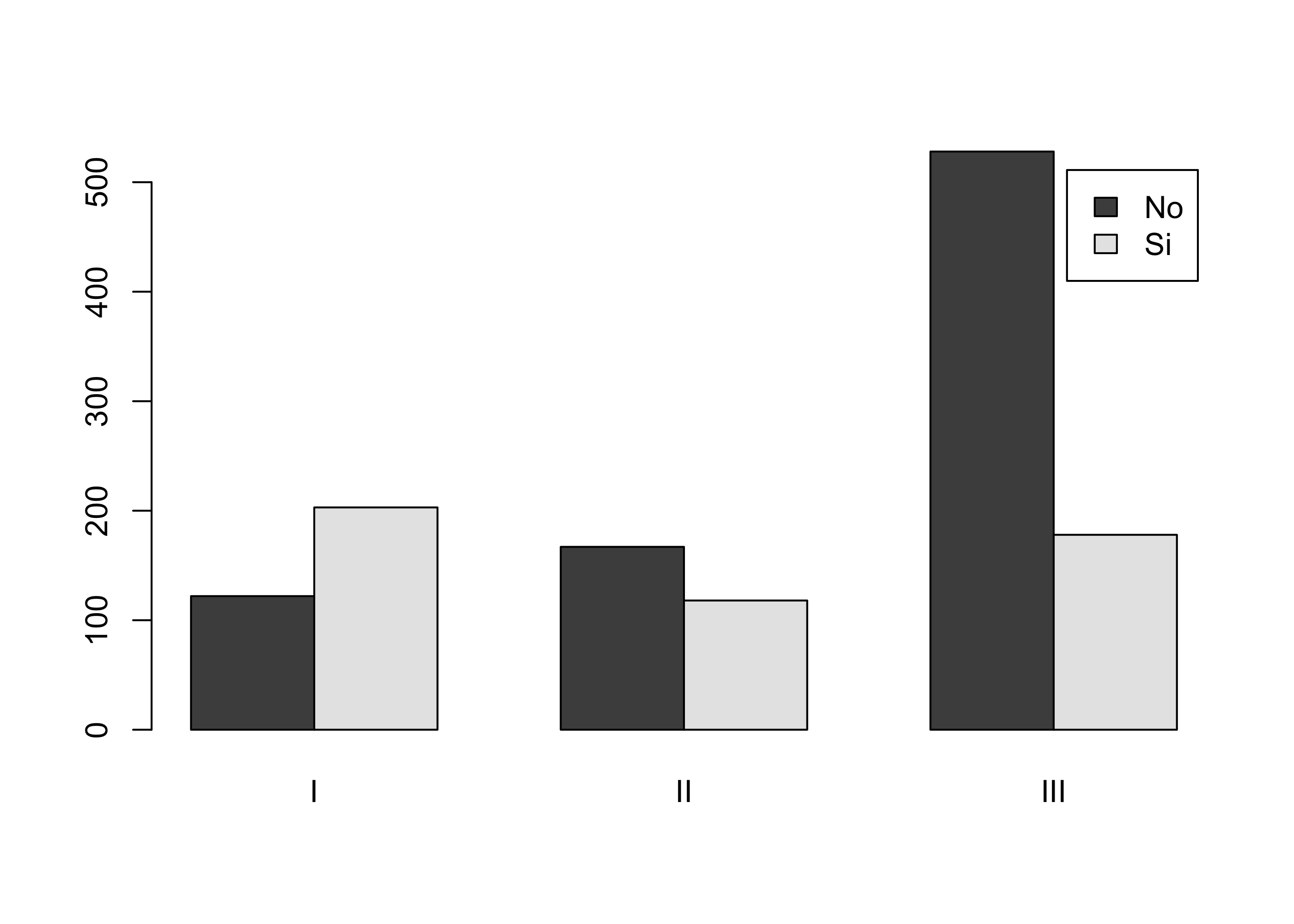

Se fossimo interessati a mostrare le frequenze condizionate, possiamo invece usare:

barplot(prop.table(tab, 2),
  beside = FALSE,
  xlab = "Classe",
  legend.text = TRUE
) # Beside = FALSE "mette in colonna" i rettangoli.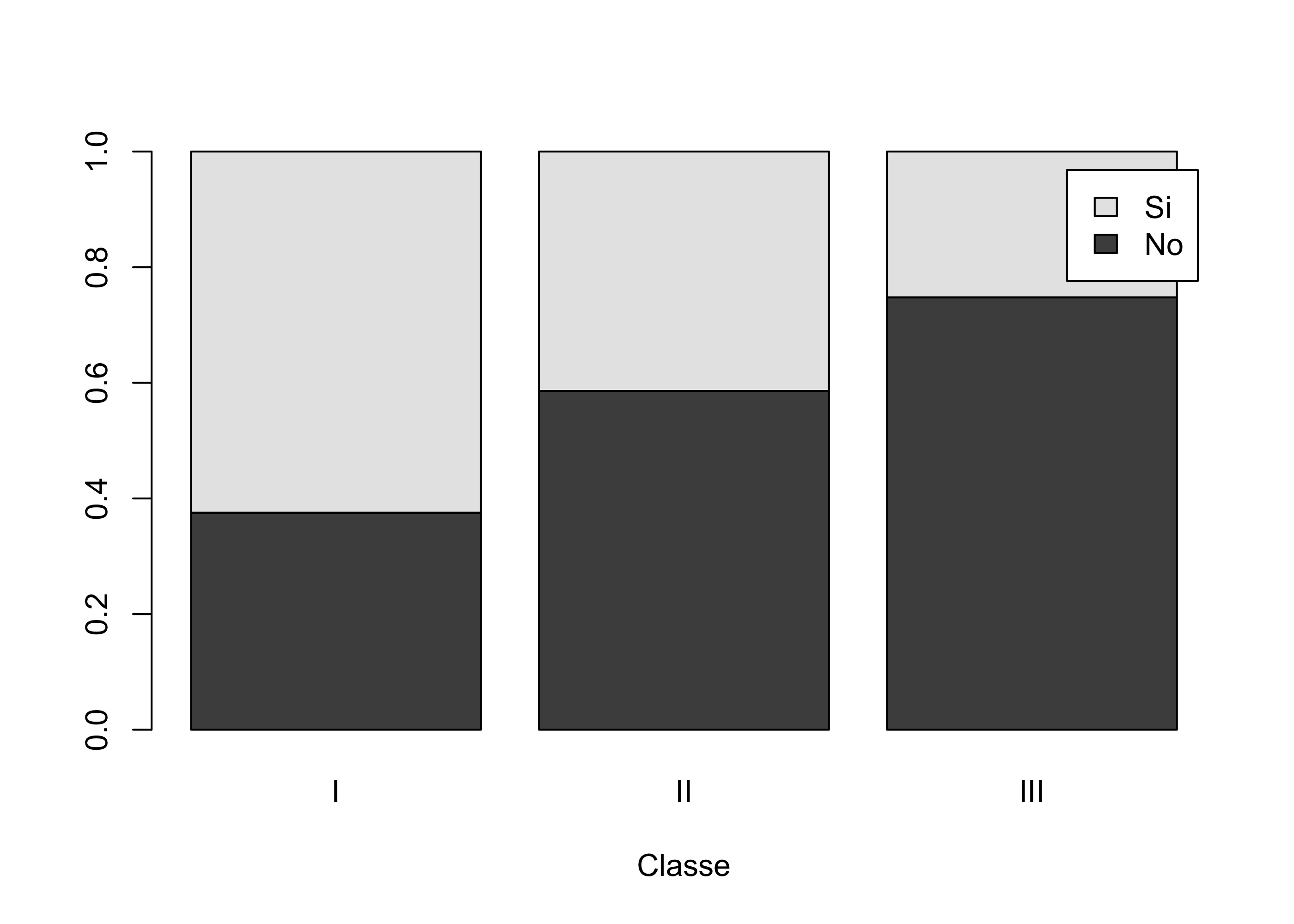

Strumenti grafici avanzati (opzionale)

Il pacchetto ggplot2

Il cosiddetto R base contiene un’ampia gamma di rappresentazioni grafiche. Ciò nonostante, un pacchetto grafico di R chiamato ggplot2 ha recentemente acquisito notevole popolarità.

Carichiamolo anzitutto in memoria:

library(ggplot2)

Quindi, il primo grafico mostrato in precedenza si può ottenere con la sintassi:

ggplot(data = titanic, aes(x = Classe, fill = Salvato)) +
  geom_bar(position = "dodge") +
  theme_bw() +
  theme(legend.position = "top") +
  scale_fill_brewer(palette = "Dark2") +
  ylab("Frequenze assolute")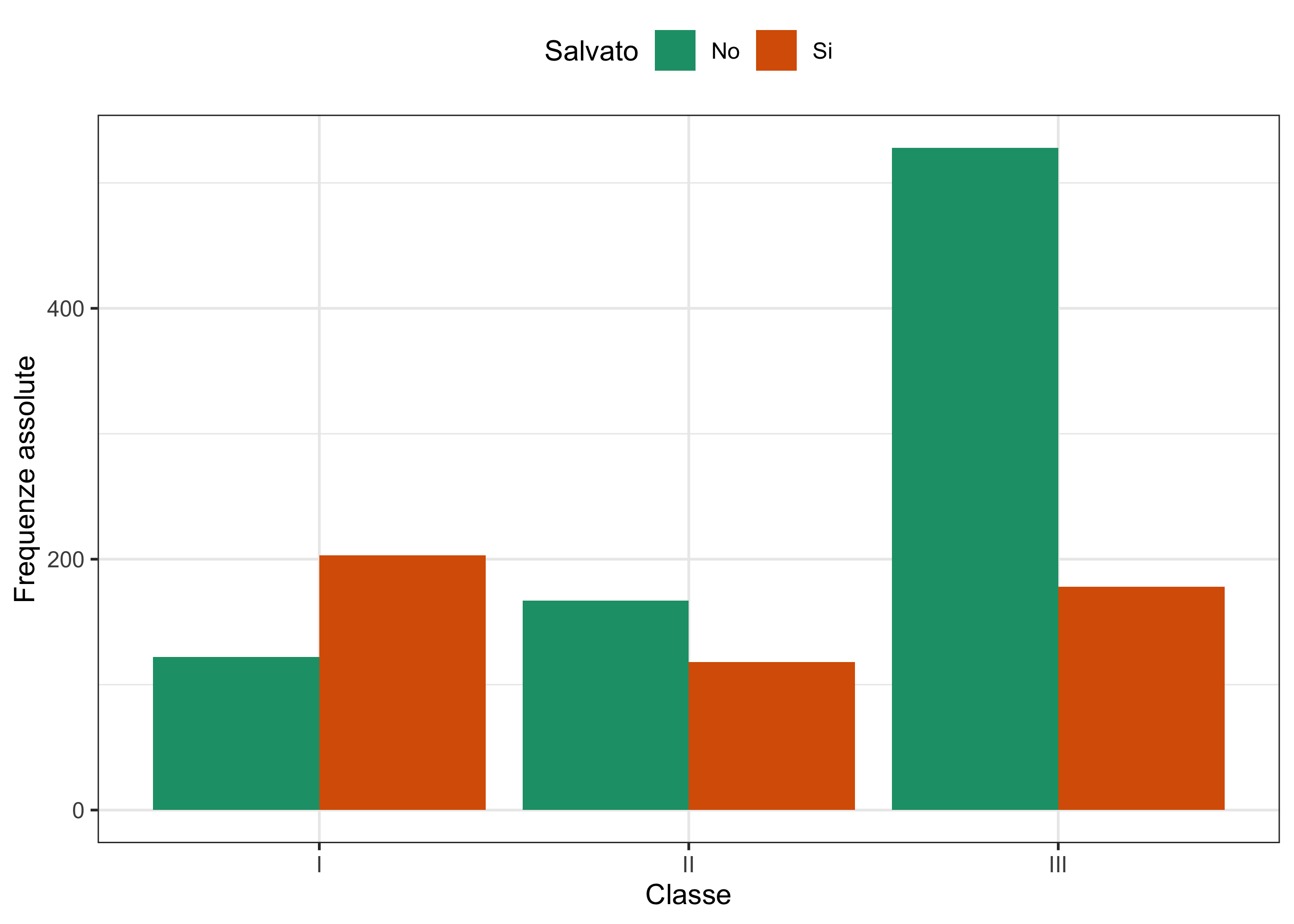

Mentre il secondo:

ggplot(data = titanic, aes(x = Classe, fill = Salvato)) +
  geom_bar(position = "fill") +
  theme_bw() +
  theme(legend.position = "top") +
  scale_fill_brewer(palette = "Dark2") +
  ylab("Frequenze relative")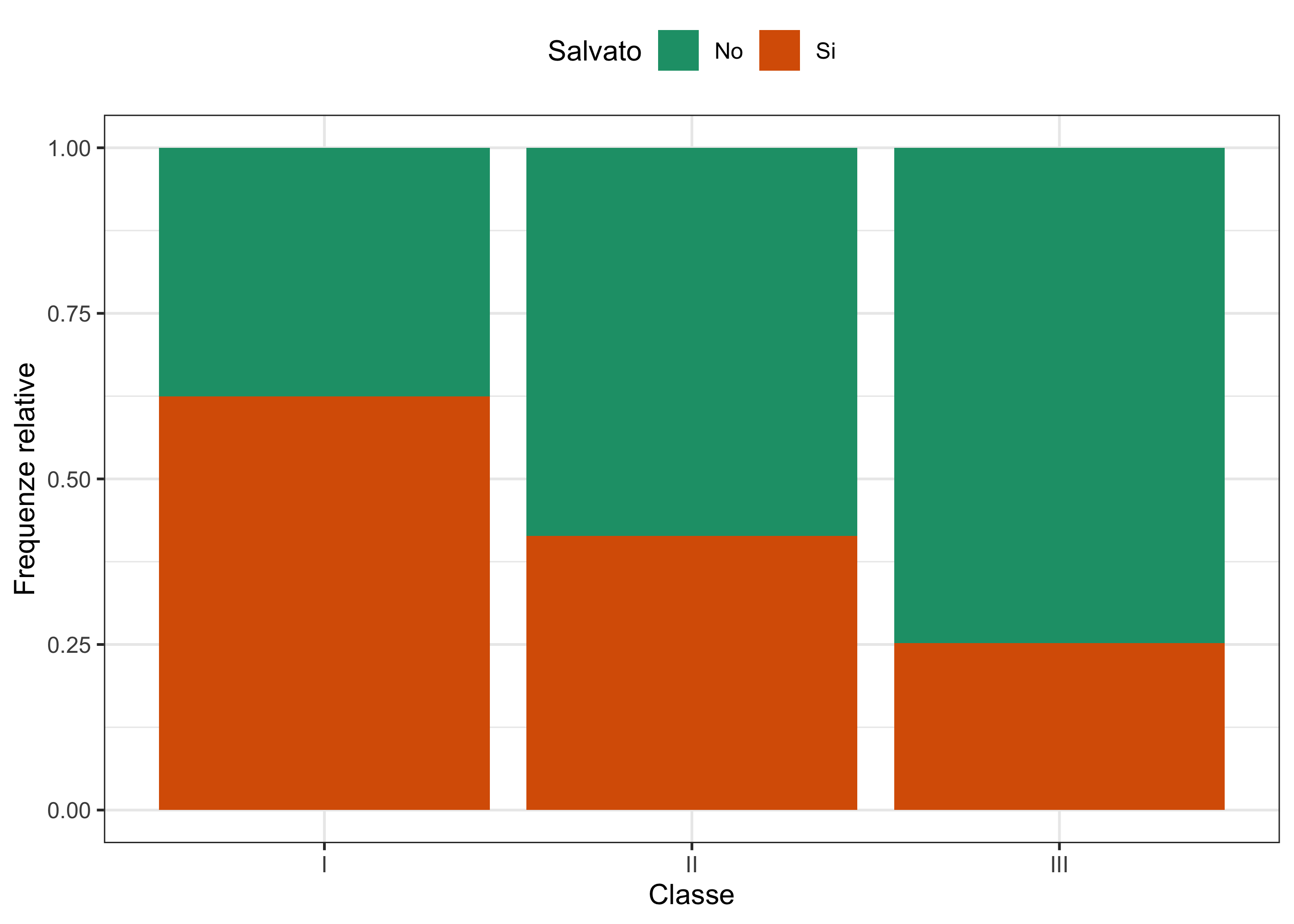

Grafici interattivi tramite Flourish

In particolar modo nell’ambito del cosiddetto data journalism, si è diffuso uno strumento per creare grafici interattivi chiamato Flourish.

Si vedano ad esempio questo articolo del Sole 24 Ore, oppure questo articolo del Post.

Il vantaggio principale della web-app Flourish è la sua semplicità d’uso. Inoltre, i grafici prodotti sono, di solito, esteticamente gradevoli.

Un esempio con i dati titanic:

Un secondo esempio con i dati titanic:

Esercizio riassuntivo

Le contingenze sono pari alla differenza tra frequenze osservate e frequenze attese, sotto l’ipotesi di indipendenza: (\text{contingenza}_{ij}) = n_{ij} - \hat{n}_{ij}, \qquad i=1,\dots,h,\quad j=1,\dots,k.

Si consulti l’unità O di Statistica I per la definizione di frequenze attese.

L’indice di connessione \chi^2 è definito come \chi^2 = \sum_{i=1}^h\sum_{j=1}^k \frac{(n_{ij} - \hat{n}_{ij})^2}{\hat{n}_{ij}} = n\left(\sum_{i=1}^h\sum_{j=1}^k\frac{f_{ij}^2}{f_{i+}f_{+j}} - 1\right).

Si scriva una funzione R chiamata chi_squared(x, y) che calcola l’indice \chi^2 di Pearson.

Soluzione

chi_squared <- function(x, y) {
  nn <- table(x, y)
  n <- sum(nn)
  ff <- nn / n # Frequenze relative congiunte
  f_x <- table(x) / n # Frequenze relative marginali di x
  f_y <- table(y) / n # Frequenze relative marginali di y
  S <- 0
  for (i in 1:length(f_x)) {
    for (j in 1:length(f_y)) {
      S <- S + ff[i, j]^2 / (f_x[i] * f_y[j])
    }
  }
  n * (S - 1)
}
chi_squared(titanic$Salvato, titanic$Classe)
     No 
133.052

Soluzione (alternativa, più concisa)

La soluzione seguente fa uso delle funzioni apply e outer.

chi_squared <- function(x, y) {
  nn <- table(x, y)
  n <- sum(nn)
  ff <- nn / n
  f_x <- apply(ff, 1, sum)
  f_y <- apply(ff, 2, sum)
  f_e <- outer(f_x, f_y) # Prodotto "esterno" tra vettori
  n * (sum(ff^2 / f_e) - 1)
}
chi_squared(titanic$Salvato, titanic$Classe)
[1] 133.052

Infine, si noti che la funzione chisq.test produce lo stesso risultato.

chisq.test(table(titanic$Salvato, titanic$Classe))

    Pearson's Chi-squared test

data:  table(titanic$Salvato, titanic$Classe)
X-squared = 133.05, df = 2, p-value < 2.2e-16