set.seed(100)
n <- 20 # Numerosità campionaria
mu <- 10 # Media teorica (solitamente ignota)
# Campione y_1,...,y_n
y <- rnorm(n, mean = mu, sd = sqrt(16))
# Vero valore è mu = 10
mean(y) [1] 10.43147median(y) [1] 10.37232R per l’analisi statistica multivariata
Unità M: proprietà degli stimatori
Argomenti affrontati
- Distribuzione di uno stimatore
- Distorsione, varianza ed errore quadratico medio
Ripasso e notazione I
In questa unità discuteremo di stimatori e delle loro proprietà.
Ricordiamo che, nel caso assolutamente continuo, un modello statistico è una collezione di funzioni di densità \mathcal{F} = \{f(\cdot; \theta) : \theta \in \Theta\}, indicizzata da un vettori di parametri \theta \in \Theta, dove \Theta \subseteq \mathbb{R}^p è lo spazio parametrico.
Assumiamo inoltre che i dati y_1,\dots,y_n siano realizzazioni iid di variabili aleatorie Y_1,\dots,Y_n con legge f(y; \theta), per un qualche ignoto valore del parametro \theta.
Il nostro scopo è stimare l’ignoto valore di \theta nel miglior modo possibile usando i dati osservati y = (y_1,\dots,y_n).
Ripasso e notazione II
Uno stimatore \hat{\theta}(Y) è una qualsiasi funzione delle variabili aleatorie Y = (Y_1,\dots, Y_n) che “si avvicina” al vero valore di \theta. Lo stimatore è una variabile aleatoria.
Una stima \hat{\theta} = \hat{\theta}(y) è una qualsiasi funzione dei dati y = (y_1,\dots,y_n) che ``si avvicina’’ al vero valore di~\theta. La stima è la realizzazione di \hat{\theta}(Y), perciò è un numero.
Abbiamo bisogno di criterio per stabilire se uno stimatore “funziona” o meno. Il sostegno logico e filosofico proviene dal seguente principio (frequentista).
Il principio del campionamento ripetuto I (ripasso)
Immaginiamo che sia possibile, almeno ipoteticamente, ripetere l’esperimento varie volte, ottenendo ogni volta un nuovo campione y e quindi una nuova stima \hat{\theta}.
Di conseguenza, lo stimatore \hat{\theta}(Y) è una variabile aleatoria, per la quale possiamo parlare di distribuzione, valore atteso e così via.
Il principio del campionamento ripetuto II (ripasso)
Se accettiamo il principio del campionamento ripetuto, valuteremo le bontà della singola stima \hat{\theta} sulla base delle proprietà dello stimatore \hat{\theta}(Y).
In altri termini, ci chiediamo come si comporterebbero le varie stime \hat{\theta} se potessimo osservare tanti campioni, non solo quello che abbiamo a disposizione.
Ci aspettiamo che mediamente la distribuzione di \hat{\theta}(Y) sia concentrata attorno al vero ed ignoto valore \theta. Ovviamente, questo non è assicurato campione per campione.
Una proprietà tipicamente richiesta è che all’aumentare della dimensione del campione n, la distribuzione di \hat{\theta}(Y) sia concentrata attorno a \theta.
Ripasso e notazione III
Una prima semplice aspettativa rispetto allo stimatore è che mediamente esso sia corretto o non distorto, ovvero \mathbb{E}\{\hat{\theta}(Y)\} = \theta, \qquad \theta \in \Theta.
La **distorsione è infatti definita come la differenza semplice \text{bias}\{\hat{\theta}(Y)\}:= \mathbb{E}\{\hat{\theta}(Y)\} - \theta, \qquad \theta \in \Theta.
Se uno stimatore è non distorto allora ovviamente \text{bias}\{\hat{\theta}(Y)\} = 0.
Un requisito un po’ meno stringente è che lo stimatore sia asintoticamente non distorto, come è tipicamente la stima di massima verosimiglianza, ovvero \lim_{n \rightarrow \infty} \mathbb{E}\{\hat{\theta}(Y)\} = \theta, \qquad \theta \in \Theta, dove n è la dimensione campionaria.
Ripasso e notazione IV
La non-distorsione (asintotica) è una proprietà auspicabile, ma spesso meno importante dello errore o scarto quadratico medio.
Lo scarto quadratico medio (mean squared error) misura la distanza media tra stimatore e vero valore del parametro, ovvero \text{MSE}\{\hat{\theta}(Y)\} = \mathbb{E}\left\{\left[\hat{\theta}(Y) - \theta\right]^2\right\}, \qquad \theta \in \Theta.
Ripasso e notazione V
Uno stimatore si dice consistente in media quadratica se \lim_{n \rightarrow \infty} \text{MSE}\{\hat{\theta}(Y)\} = 0, \qquad \theta \in \Theta. oppure equivalentemente se \lim_{n \rightarrow \infty} \mathbb{E}\{\hat{\theta}(Y)\} = \theta, \quad \lim_{n \rightarrow \infty} \text{var}\{\hat{\theta}(Y)\} = 0, \qquad \theta \in \Theta.
La consistenza in media quadratica implica la convergenza in probabilità, per cui scriveremo che \hat{\theta}(Y) \overset{p}{\longrightarrow} \theta, \qquad n \rightarrow \infty, \qquad \theta \in \Theta.
Esercizio
Lo studente è invitato a rivedersi la definizione di convergenza in probabilità, le sue proprietà e la sua relazione con la consistenza in media quadratica (in L^2).
Inferenza statistica e metodi Monte Carlo
Stabiliti i criteri per valutare la bontà di uno stimatore, rimane da capire come utilizzarli in pratica.
Nei corsi di Statistica II vengono presentati modelli e stimatori per i quali è possibile calcolare l’MSE analiticamente. Questo capita di rado nelle applicazioni reali.
Fortunatamente il metodo Monte Carlo che abbiamo visto nell’unità I può venire in aiuto in assenza di risultati analitici.
Ad esempio, lo scarto quadratico medio è per definizione un valore atteso, che possiamo quindi approssimare tramite integrazione Monte Carlo.
Modello gaussiano con varianza nota I
Sia y = (y_1,\dots,y_n) un campione iid da una variabile casuale normale con media ignota \mu e varianza nota e pari \sigma^2 = 16, ovvero Y \sim \text{N}(\mu, 16).
Il parametro \mu è ignoto e siamo interessati a stimarlo.
Uno stima naturale per \mu, che oltretutto coincide con la SMV, è la media aritmetica \hat{\mu} = \frac{1}{n}\sum_{i=1}^n y_i.
La distribuzione (esatta!) dello stimatore \hat{\mu}(Y) è nota ed è pari \hat{\mu}(Y) \sim \text{N}\left(\mu, \frac{16}{n}\right).
Esercizio
Si dimostri che \text{MSE}\{\hat{\mu}(Y)\} = 16 / n. Se ne deduca che lo stimatore è consistente.
Modello gaussiano con varianza nota II
Un secondo possibile stimatore per \mu è la mediana campionaria .
La distribuzione dello stimatore \text{Me}(Y) è ignota. Di conseguenza, anche le relative proprietà sono ignote.
La mediana è uno stimatore distorto? Il suo scarto è maggiore o minore di quello della media aritmetica?
In assenza di risultati analitici, possiamo provare a fornire una risposta parziale tramite Monte Carlo.
In altri termini, indagheremo quale stimatore funziona meglio per degli specifici valori di \mu, ad esempio \mu = 10 oppure \mu = 15.
Modello gaussiano con varianza nota III
Supponiamo di voler investigare il caso \mu = 10. Supponiamo inoltre che n = 20.
Cominciamo simulando un singolo campione y_1,\dots,y_n da una distribuzione \text{N}(\mu, 16).
In questo caso specifico, la mediana si avvicina di più al vero valore della media (\mu = 10). Tuttavia, questo vale per questo specifico campione.
Modello gaussiano con varianza nota IV
Coerentemente con quanto discusso nei paragrafi precedenti, un modo preciso per valutare la bontà dello stimatore si basa sul campionamento ripetuto.
In altri termini, vogliamo confrontare gli scarti quadratici medi dei due stimatori \text{MSE}\{\hat{\mu}(Y)\}, \qquad \text{MSE}\{\text{Me}(Y)\}.
Nel caso della media aritmetica con \sigma^2 = 16 ed n = 20 i conti analitici implicano che \text{MSE}\{\hat{\mu}(Y)\} = 16 / 20 = 0.8. Ma nel caso della mediana?
Utilizzando il metodo Monte Carlo, ottengo una stima dello scarto quadratico medio dello stimatore mediana, ovvero \widehat{\text{MSE}\{\text{Me}(Y)\}}.
Esercizio
Lo studente rilegga questa frase fino a convincersi della sua correttezza.
Modello gaussiano con varianza nota V
L’approssimazione \widehat{\text{MSE}\{\text{Me}(Y)\}} si basa sul metodo di integrazione Monte Carlo.
Si supponga che \text{Me}_1, \dots, \text{Me}_R siano R estrazioni casuali della mediana calcolata su un campione iid gaussiano (\mu = 10, \sigma^2 = 16) di dimensione n = 20.
Possiamo ottenere \text{Me}_1, \dots, \text{Me}_R simulando R campioni Y e calcolandone la mediana:
set.seed(156)
R <- 10^5
# Ottengo R estrazioni della mediana campionaria Me_1,...Me_R
median_hat <- replicate(R, median(rnorm(n = n, mean = mu, sd = sqrt(16))))L’approssimazione Monte Carlo è quindi pari a \widehat{\text{MSE}\{\text{Me}(Y)\}} = \frac{1}{R}\sum_{r=1}^R(\text{Me}_r - \mu)^2 \approx \mathbb{E}\{ (\text{Me}(Y) - \mu)^2\} = \text{MSE}\{\text{Me}(Y)\}.
mean((median_hat - mu)^2) # Stima dello scarto quadratico medio (MSE) della mediana[1] 1.172079Modello gaussiano con varianza nota VI
La mediana sembra essere meno efficiente della media aritmetica, quantomeno se \mu = 10, \sigma^2 =16 ed n = 20.
Nel seguito sono riportati alcuni risultati aggiuntivi, incluse le stime Monte Carlo relative alla media aritmetica.
set.seed(156)
R <- 10^5
mu_hat <- replicate(R, mean(rnorm(n = n, mean = mu, sd = sqrt(16))))
median_hat <- replicate(R, median(rnorm(n = n, mean = mu, sd = sqrt(16))))
mean(mu_hat) - mu # Distorsione dello stimatore; valore teorico: 0[1] -0.004089293mean((mu_hat - mu)^2) # Scarto quadratico medio dello stimatore; valore teorico: 0.8[1] 0.8008738mean(median_hat) - mu # Distorsione dello stimatore; valore teorico: ??[1] -0.001820327mean((median_hat - mu)^2) # Scarto quadratico medio dello stimatore; valore teorico: ??[1] 1.172248Distribuzione degli stimatori
par(mfrow = c(1, 2))
hist(mu_hat, breaks = 100, freq = F)
hist(median_hat, breaks = 100, freq = F)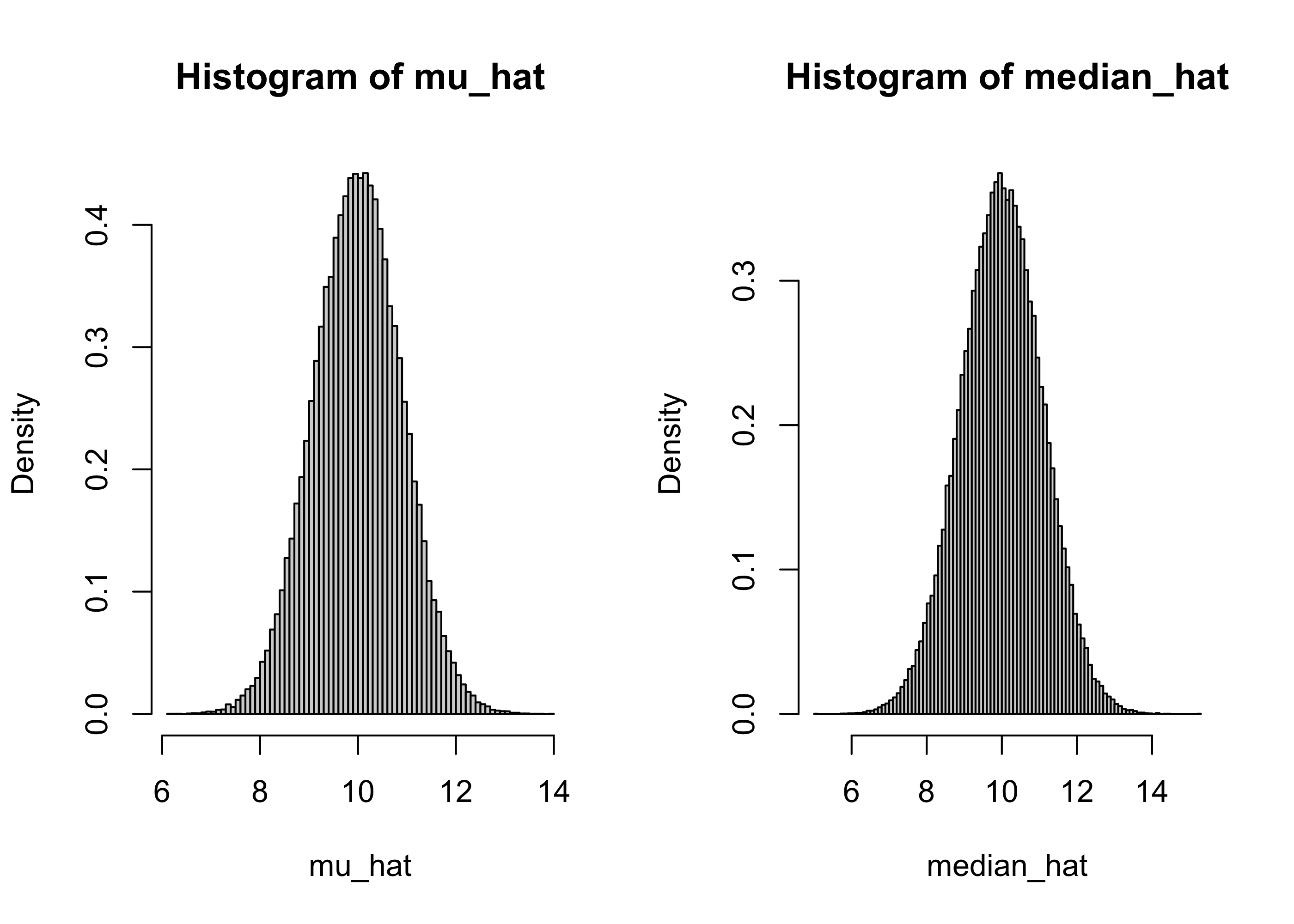
Commenti conclusivi
Le approssimazioni coinvolte in questa ultima discussione sono di due differenti tipologie.
Da un lato abbiamo la variabilità di \hat{\theta}, che è legata ai dati y_1,\dots,y_n e alla loro numerosità campionaria n.
Dall’altro abbiamo la variabilità Monte Carlo di \widehat{\text{MSE}\{\theta(Y)\}}, che è invece legata alle repliche Monte Carlo e al numero di simulazioni R.
Questi due concetti sono ben distinti e non vanno confusi tra loro.
Inoltre, mentre aumentare il numero di simulazioni R è sempre possibile (basta aspettare più tempo), non sempre disponiamo di dati aggiuntivi.
Esercizio riassuntivo
Si supponga che Y_1,\dots,Y_n sono variabili aleatorie iid distribuite come un normale di media nota \mathbb{E}(Y_1) = 0, con n = 20.
La varianza \sigma^2 è ignota e siamo interessati a stimarla.
Si calcolino tramite simulazione la distorsione e l’errore quadratico dei seguenti stimatori della varianza, quando \sigma^2 = 16:
\begin{aligned} &S^2_1 = \frac{1}{n}\sum_{i=1}^n(Y_i - \bar{Y})^2, &&\quad S^2_2 = \frac{1}{n -1}\sum_{i=1}^n(Y_i - \bar{Y})^2, \\ &S^2_3 = \frac{1}{n}\sum_{i=1}^nY_i^2, && \quad S_4 = \frac{1}{n+1}\sum_{i=1}^n(Y_i - \bar{Y})^2. \end{aligned}
Schema della soluzione
set.seed(520)
R <- 10^5; n <- 20
mu <- 0; sigma2 <- 16
# Definisco le funzioni che calcolano gli stimatori
var1 <- function(x) mean(x^2) - mean(x)^2
var2 <- function(x) var(x) # Coincide con la definizione di R
var3 <- function(x) mean(x^2)
var4 <- function(x) (length(x) - 1) / (length(x) + 1) * var(x)
# Esecuzione della simulazione
S2_1 <- replicate(R, var1(rnorm(n = n, mean = mu, sd = sqrt(sigma2))))
S2_2 <- replicate(R, var2(rnorm(n = n, mean = mu, sd = sqrt(sigma2))))
S2_3 <- replicate(R, var3(rnorm(n = n, mean = mu, sd = sqrt(sigma2))))
S2_4 <- replicate(R, var4(rnorm(n = n, mean = mu, sd = sqrt(sigma2))))
# Distorsioni (approssimate)
round(mean(S2_1 - sigma2), 2)[1] -0.85round(mean(S2_2 - sigma2), 2)[1] 0round(mean(S2_3 - sigma2), 2)[1] -0.03round(mean(S2_4 - sigma2), 2)[1] -1.56# Errore quadratico medio (approssimato)
mean((S2_1 - sigma2)^2)[1] 24.96644mean((S2_2 - sigma2)^2)[1] 27.09368mean((S2_3 - sigma2)^2)[1] 25.40207mean((S2_4 - sigma2)^2)[1] 24.36703Consistenza I
Sia y_1,\dots,y_n un campione iid da una distribuzione uniforme in (0,\theta), dove \theta > 0 è un parametro ignoto. La stima di massima verosimiglianza in questo caso è pari a \hat{\theta}_n = \max\{X_1,\dots,X_n\}.
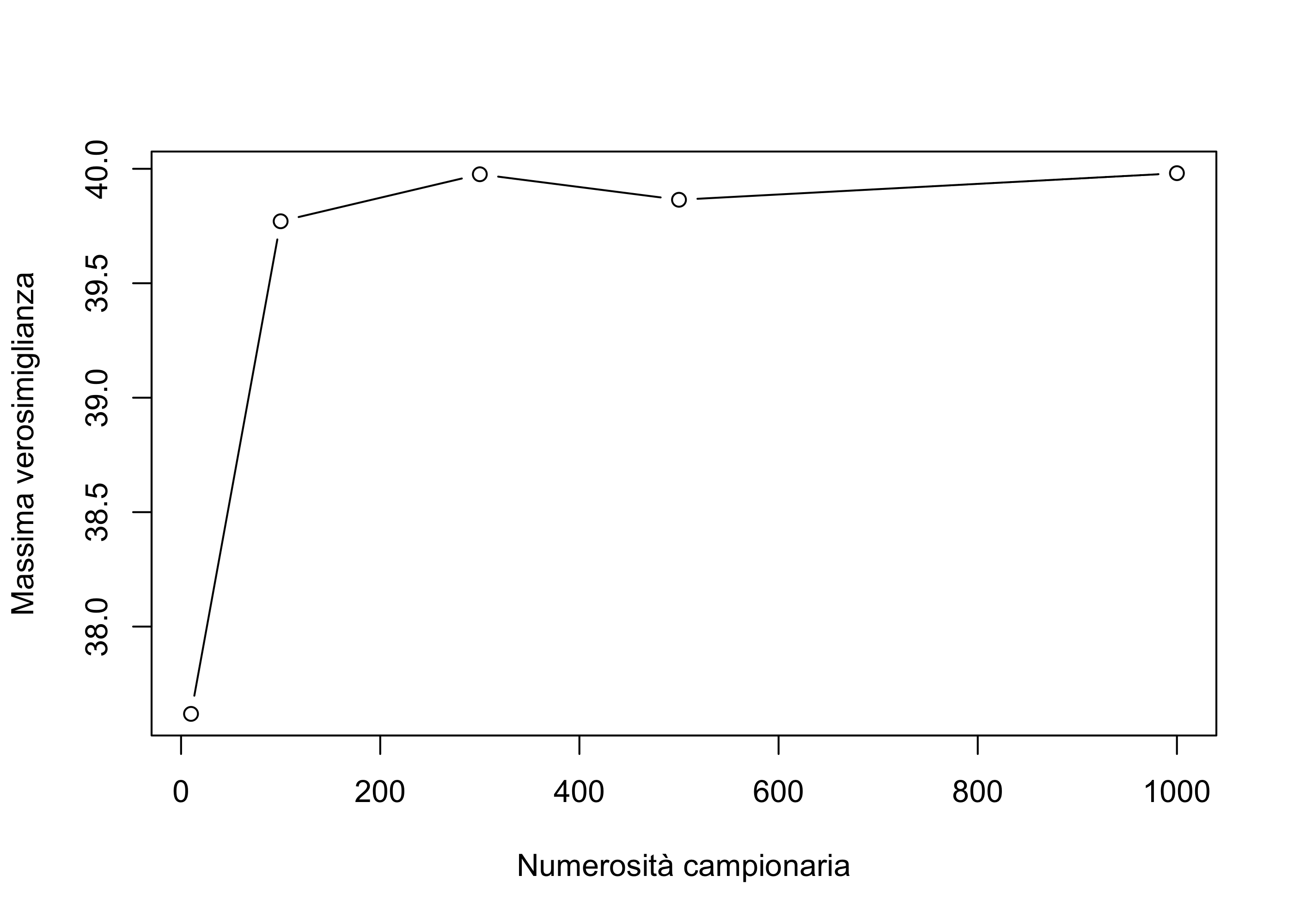
Vogliamo verificare tramite simulazione se lo stimatore è consistente, ovvero se \hat{\theta}(Y) \overset{p}{\longrightarrow} \theta.
In pratica, ciò che possiamo fare è simulare alcuni valori di \hat{\theta} per valori di n crescenti e controllare se questi si avvicinano sempre più a \theta.
Consistenza II
Supponiamo che il vero valore del parametro sia \theta = 40.
theta0 <- 40
# Numerosità campionarie
nn <- c(10, 100, 300, 500, 1000)
# Stime di massima verosimiglianza
set.seed(123)
theta_hat <- c(
max(runif(nn[1], min = 0, max = theta0)),
max(runif(nn[2], min = 0, max = theta0)),
max(runif(nn[3], min = 0, max = theta0)),
max(runif(nn[4], min = 0, max = theta0)),
max(runif(nn[5], min = 0, max = theta0))
)
theta_hat[1] 37.61869 39.77079 39.97618 39.86469 39.98096All’aumentare di n, lo stimatore tende a diventare sempre più preciso. Per valori di n ancora maggiori di 1000, la precisione aumenta ulteriormente.
Consistenza III
par(mfrow=c(1,1))
plot(nn, theta_hat,
type = "b",
xlab = "Numerosità campionaria",
ylab = "Massima verosimiglianza"
)